链表Tag

链表理论基础
什么是链表，链表是一种通过指针串联在一起的线性结构，每一个结点由两部分组成，一个是数据域一个是指针域（存放指向下一个结点的指针），最后一个结点的指针域指向null（空指针的意思）。
链表的入口结点称为链表的头结点也就是head。
……

链表

链表理论基础

什么是链表，链表是一种通过指针串联在一起的线性结构，每一个结点由两部分组成，一个是数据域一个是指针域（存放指向下一个结点的指针），最后一个结点的指针域指向null（空指针的意思）。
链表的入口结点称为链表的头结点也就是head。

链表的类型

单链表：即为前面的图，单链表中的指针域只能指向结点的下一个结点。
双链表：每一个结点有两个指针域，一个指向下一个结点，一个指向上一个结点。双链表既可以向前查询也可以向后查询。
循环链表：顾名思义，就是链表首尾相连。循环链表可以用来解决约瑟夫环问题。

链表的存储方式

了解完链表的类型，再来说一说链表在内存中的存储方式。
数组是在内存中是连续分布的，但是链表在内存中可不是连续分布的。链表是通过指针域的指针链接在内存中各个结点。所以链表中的结点在内存中不是连续分布的，而是散乱分布在内存中的某地址上，分配机制取决于操作系统的内存管理。
如图所示：
这个链表起始结点为2，终止结点为7，各个结点分布在内存的不同地址空间上，通过指针串联在一起。

链表的定义

接下来说一说链表的定义。链表结点的定义，很多同学在面试的时候都写不好。这是因为平时在刷leetcode的时候，链表的结点都默认定义好了，直接用就行了，所以同学们都没有注意到链表的结点是如何定义的。而在面试的时候，一旦要自己手写链表，就写的错漏百出。

public class ListNode {
    // 结点的值
    int val;

    // 下一个结点
    ListNode next;

    // 结点的构造函数(无参)
    public ListNode() {
    }

    // 结点的构造函数(有一个参数)
    public ListNode(int val) {
        this.val = val;
    }

    // 结点的构造函数(有两个参数)
    public ListNode(int val, ListNode next) {
        this.val = val;
        this.next = next;
    }
}

链表的操作

删除结点

删除D结点，如图所示：
只要将C结点的next指针指向E结点就可以了。
那有同学说了，D结点不是依然存留在内存里么？只不过是没有在这个链表里而已。
是这样的，所以在C++里最好是再手动释放这个D结点，释放这块内存。
其他语言例如Java、Python，就有自己的内存回收机制，就不用自己手动释放了。

添加结点

添加F结点，如图所示：
可以看出链表的增添和删除都是O(1)操作，也不会影响到其他结点。
但是要注意，要是删除第五个结点，需要从头结点查找到第四个结点通过next指针进行删除操作，**查找的时间复杂度是O(n)**。

性能分析

再把链表的特性和数组的特性进行一个对比，如图所示：
数组在定义的时候，长度就是固定的，如果想改动数组的长度，就需要重新定义一个新的数组。
链表的长度可以是不固定的，并且可以动态增删，适合数据量不固定，频繁增删，较少查询的场景。

1. 移除链表元素

题目

给你一个链表的头结点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的结点，并返回 新的头结点 。
示例 1：
1
2
输入：head = [1,2,6,3,4,5,6], val = 6
输出：[1,2,3,4,5]
示例 2：
1
2
输入：head = [], val = 1
输出：[]
示例 3：
1
2
输入：head = [7,7,7,7], val = 7
输出：[]
提示：
- 列表中的结点数目在范围 [0, 104] 内
- 1 <= Node.val <= 50
- 0 <= val <= 50

思路

一般情况下，如果当前结点是要删除的结点，那么让当前结点的前一个结点的next指针直接指向当前结点的下一个结点即可。
但是如果头结点是要删除的结点，就可以有两种方式对链表进行操作：
1. 直接使用原来的链表来进行删除操作。
2. 设置一个虚拟头结点再进行删除操作。

方式1：直接使用原来的链表来进行删除操作。

该方式需要增加一段业务逻辑：
移除头结点和移除其他结点的操作是不一样的，因为链表的其他结点都是通过前一个结点来移除当前结点，而头结点没有前一个结点。
所以头结点如何移除呢，其实只要将头结点向后移动一位就可以，这样就从链表中移除了一个头结点。

代码如下：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 * int val;
 * ListNode next;
 * ListNode() {}
 * ListNode(int val) { this.val = val; }
 * ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeElements(ListNode head, int val) {
        //移除头结点
        while (head != null && head.val == val) {
            head = head.next;
        }
        if (head == null) {
            return null;
        }
        ListNode pre = head;
        ListNode cur = head.next;
        while (cur != null) {
            if (cur.val == val) {
                pre.next = cur.next;
            } else {
                pre = cur;
            }
            cur = cur.next;
        }
        return head;
    }
}

★虚拟头结点

方式2：设置一个虚拟头结点再进行删除操作。

这种方式的好处是将删除头结点这种特殊的情况转变为一般的情况，让我们可以以一种统一的逻辑来移除链表的结点。
最后记得在题目中，return 头结点的时候，别忘了 return dummyHead.next;，这才是新的头结点。

代码如下：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 * int val;
 * ListNode next;
 * ListNode() {}
 * ListNode(int val) { this.val = val; }
 * ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeElements(ListNode head, int val) {
        if (head == null) {
            return null;
        }
        //添加虚拟头结点
        ListNode dummyHead = new ListNode(-1, head);
        ListNode pre = dummyHead;
        ListNode cur = head;
        while (cur != null) {
            if (cur.val == val) {
                pre.next = cur.next;
            } else {
                pre = cur;
            }
            cur = cur.next;
        }
        return dummyHead.next;
    }
}

2.设计链表

题目

你可以选择使用单链表或者双链表，设计并实现自己的链表。
单链表中的结点应该具备两个属性：val 和 next 。val 是当前结点的值，next 是指向下一个结点的指针/引用。
如果是双向链表，则还需要属性 prev 以指示链表中的上一个结点。假设链表中的所有结点下标从 0 开始。

实现 MyLinkedList 类：

MyLinkedList() 初始化 MyLinkedList 对象。
int get(int index) 获取链表中下标为 index 的结点的值。如果下标无效，则返回 -1 。
void addAtHead(int val) 将一个值为 val 的结点插入到链表中第一个元素之前。在插入完成后，新结点会成为链表的第一个结点。
void addAtTail(int val) 将一个值为 val 的结点追加到链表中作为链表的最后一个元素。
void addAtIndex(int index, int val) 将一个值为 val 的结点插入到链表中下标为 index 的结点之前。如果 index 等于链表的长度，那么该结点会被追加到链表的末尾。如果 index 比长度更大，该结点将 不会插入 到链表中。
void deleteAtIndex(int index) 如果下标有效，则删除链表中下标为 index 的结点。

示例：

输入
["MyLinkedList", "addAtHead", "addAtTail", "addAtIndex", "get", "deleteAtIndex", "get"]
[[], [1], [3], [1, 2], [1], [1], [1]]
输出
[null, null, null, null, 2, null, 3]

解释
MyLinkedList myLinkedList = new MyLinkedList();
myLinkedList.addAtHead(1);
myLinkedList.addAtTail(3);
myLinkedList.addAtIndex(1, 2);    // 链表变为 1->2->3
myLinkedList.get(1);              // 返回 2
myLinkedList.deleteAtIndex(1);    // 现在，链表变为 1->3
myLinkedList.get(1);              // 返回 3

提示：

0 <= index, val <= 1000
请不要使用内置的 LinkedList 库。
调用 get、addAtHead、addAtTail、addAtIndex 和 deleteAtIndex 的次数不超过 2000 。

思路

单链表实现：

//单链表
class ListNode {
    int val;
    ListNode next;

    public ListNode() {

    }

    public ListNode(int val) {
        this.val = val;
    }

    public ListNode(int val, ListNode next) {
        this.val = val;
        this.next = next;
    }
}

class MyLinkedList {
    //链表中元素的个数
    int size;
    //虚拟头结点
    ListNode dummyHead;

    //初始化链表
    public MyLinkedList() {
        size = 0;
        dummyHead = new ListNode(-1, null);
    }

    public int get(int index) {
        if (index < 0 || index >= size) {
            return -1;
        }
        ListNode cur = dummyHead.next;
        for (int i = 0; i < index; i++) {
            cur = cur.next;
        }
        return cur.val;
    }

    public void addAtHead(int val) {
        addAtIndex(0, val);
    }

    public void addAtTail(int val) {
        addAtIndex(size, val);
    }

    public void addAtIndex(int index, int val) {
        if (index < 0 || index > size) {
            return;
        }
        ListNode pre = dummyHead;
        ListNode cur = dummyHead.next;
        for (int i = 0; i < index; i++) {
            pre = cur;
            cur = cur.next;
        }
        ListNode node = new ListNode(val);
        pre.next = node;
        node.next = cur;
        size++;
    }

    public void deleteAtIndex(int index) {
        if (index < 0 || index >= size) {
            return;
        }
        ListNode pre = dummyHead;
        ListNode cur = dummyHead.next;
        for (int i = 0; i < index; i++) {
            pre = cur;
            cur = cur.next;
        }
        pre.next = cur.next;
        size--;
    }
}

/**
 * Your MyLinkedList object will be instantiated and called as such:
 * MyLinkedList obj = new MyLinkedList();
 * int param_1 = obj.get(index);
 * obj.addAtHead(val);
 * obj.addAtTail(val);
 * obj.addAtIndex(index,val);
 * obj.deleteAtIndex(index);
 */

抓住核心：index 指向的是要处理的结点。

双链表实现：

//双链表
class ListNode {
    int val;
    ListNode next, prev;

    public ListNode() {
    }

    public ListNode(int val) {
        this.val = val;
    }

    public ListNode(int val, ListNode prev, ListNode next) {
        this.val = val;
        this.prev = prev;
        this.next = next;
    }
}

class MyLinkedList {
    //链表中元素的个数
    int size;
    //虚拟头结点
    ListNode dummyHead, dummyTail;

    //初始化链表
    public MyLinkedList() {
        size = 0;
        dummyHead = new ListNode(-1);
        dummyTail = new ListNode(-1, dummyHead, null);
        dummyHead.prev = null;
        dummyHead.next = dummyTail;
    }

    public int get(int index) {
        if (index < 0 || index >= size) {
            return -1;
        }
        ListNode cur;
        //判断哪一边遍历的时间更短
        if (index <= size / 2) {
            cur = dummyHead.next;
            for (int i = 0; i < index; i++) {
                cur = cur.next;
            }
        } else {
            cur = dummyTail.prev;
            for (int i = size - 1; i > index; i--) {
                cur = cur.prev;
            }
        }
        return cur.val;
    }

    public void addAtHead(int val) {
        addAtIndex(0, val);
    }

    public void addAtTail(int val) {
        addAtIndex(size, val);
    }

    public void addAtIndex(int index, int val) {
        if (index < 0 || index > size) {
            return;
        }
        ListNode pre = dummyHead;
        ListNode cur = dummyHead.next;
        for (int i = 0; i < index; i++) {
            pre = cur;
            cur = cur.next;
        }
        ListNode node = new ListNode(val);
        pre.next = node;
        node.prev = pre;
        node.next = cur;
        cur.prev = node;
        size++;
    }

    public void deleteAtIndex(int index) {
        if (index < 0 || index >= size) {
            return;
        }
        ListNode pre = dummyHead;
        ListNode cur = dummyHead.next;
        for (int i = 0; i < index; i++) {
            pre = cur;
            cur = cur.next;
        }
        pre.next = cur.next;
        cur.next.prev = pre;
        size--;
    }
}

/**
 * Your MyLinkedList object will be instantiated and called as such:
 * MyLinkedList obj = new MyLinkedList();
 * int param_1 = obj.get(index);
 * obj.addAtHead(val);
 * obj.addAtTail(val);
 * obj.addAtIndex(index,val);
 * obj.deleteAtIndex(index);
 */

3.★反转链表

题目

给你单链表的头结点 head ，请你反转链表，并返回反转后的链表。
示例 1：
1
2
输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]
示例 2：
1
2
输入：head = [1,2]
输出：[2,1]
示例 3：
1
2
输入：head = []
输出：[]
提示：
- 链表中结点的数目范围是 [0, 5000]
- -5000 <= Node.val <= 5000

思路

首先定义一个cur指针，指向头结点，再定义一个pre指针，初始化为null。

然后就要开始反转了，首先要把 cur.next 结点用tmp指针保存一下，也就是保存一下这个结点。

为什么要保存一下这个结点呢，因为接下来要改变 cur.next 的指向了，将 cur.next 指向 pre ，此时已经反转了第一个结点了，为了让 cur 能指向下一个要反转的结点，就要用 tmp 保存这个结点。

接下来，就是循环走如下代码逻辑了，继续移动pre和cur指针。

最后，cur 指针已经指向了null，循环结束，链表也反转完毕了。此时我们return pre指针就可以了，pre指针就指向了新的头结点。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
//双指针法
class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode pre, cur, tmp;
        pre = null;
        cur = head;
        tmp = null;
        while (cur != null) {
            //用 tmp 先保存当前结点的下一个结点
            tmp = cur.next;
            cur.next = pre;
            pre = cur;
            cur = tmp;
        }
        return pre;
    }
}

还有一种递归的方法（核心思想和前面的迭代法是一样的）：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
 //递归法
class Solution {
    public ListNode reverseList(ListNode head) {
        return reverse(null, head);
    }

    private ListNode reverse(ListNode prev, ListNode cur) {
        if (cur == null) {
            return prev;    //返回反转以后的头指针
        }
        ListNode tmp = cur.next;
        cur.next = prev;
        return reverse(cur, tmp);
    }
}

3.2 反转链表 II

题目

给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表结点，返回 反转后的链表 。
示例 1：
1
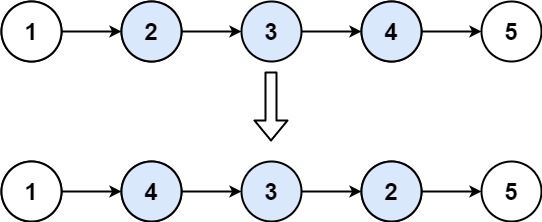
2
输入：head = [1,2,3,4,5], left = 2, right = 4
输出：[1,4,3,2,5]
示例 2：
1
2
输入：head = [5], left = 1, right = 1
输出：[5]
提示：
- 链表中结点数目为 n
- 1 <= n <= 500
- -500 <= Node.val <= 500
- 1 <= left <= right <= n

思路

和 3.反转链表 的不同之处在于，需要额外定义两个指针，分别指向 left - 1 所在的结点和 left 所在的结点，才能完成链表的部分反转。

class Solution {
    public ListNode reverseBetween(ListNode head, int left, int right) {
        if (head == null || head.next == null) { // 排除特殊情况
            return head;
        }
        ListNode dummyHead = new ListNode(-1, head); // 增加一个虚拟头结点
        ListNode pre, cur, next, temp1, temp2;
        temp1 = dummyHead;
        for (int i = 0; i < left - 1; i++) {
            temp1 = temp1.next; // temp1用于指向left左边的结点
        }
        temp2 = temp1.next; // temp2用于指向left所在的结点
        pre = temp2;
        cur = temp2.next;
        for (int i = 0; i < right - left; i++) { // 反转的次数
            next = cur.next;
            cur.next = pre;
            pre = cur;
            cur = next;
        }
        temp1.next = pre;
        temp2.next = cur;
        return dummyHead.next;
    }
}

3.3 K个一组翻转链表

题目

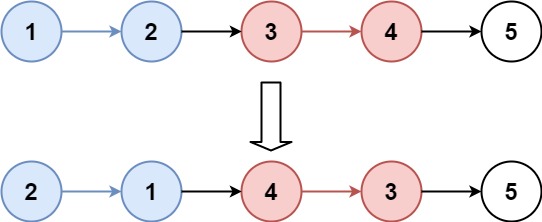
给你链表的头结点 head ，每 k 个结点一组进行翻转，请你返回修改后的链表。
k 是一个正整数，它的值小于或等于链表的长度。如果结点总数不是 k 的整数倍，那么请将最后剩余的结点保持原有顺序。
你不能只是单纯的改变结点内部的值，而是需要实际进行结点交换。
示例 1：
1
2
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]
示例 2：
1
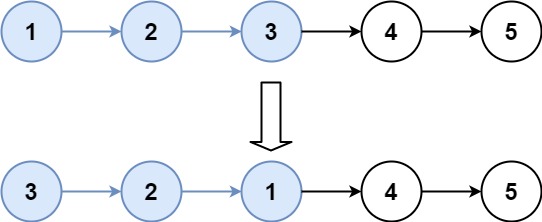
2
输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]
提示：
- 链表中的结点数目为 n
- 1 <= k <= n <= 5000
- 0 <= Node.val <= 1000
进阶：你可以设计一个只用 O(1) 额外内存空间的算法解决此问题吗？

思路

这题是在 3.2 反转链表 II 的基础上更进一步，对多组子段进行反转。

class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        // 虚拟头结点
        ListNode dummyHead = new ListNode();
        dummyHead.next = head;
        ListNode pre, cur, next, temp1, temp2;
        pre = dummyHead;
        cur = pre.next;
        int n, loop;
        n = 0;
        while (cur != null) {
            n++;
            cur = cur.next;
        }
        loop = n / k; // 计算要翻转几段
        cur = pre.next;
        for (int i = 0; i < loop; i++) {
            // 单段翻转逻辑
            temp1 = pre;
            temp2 = cur;
            for (int j = 0; j < k; j++) {
                next = cur.next;
                cur.next = pre;
                pre = cur;
                cur = next;
            }
            temp1.next = pre;
            temp2.next = cur;
            pre = temp2; // 需要让新一段开始的pre指向上一段的最后一个结点
        }
        return dummyHead.next;
    }
}

需要注意的是，在上一段翻转完后，要让下一段开始的 pre 指向上一段的最后一个结点。

4.两两交换链表中的结点

题目

给你一个链表，两两交换其中相邻的结点，并返回交换后链表的头结点。你必须在不修改结点内部的值的情况下完成本题（即，只能进行结点交换）。
示例 1：
1
2
输入：head = [1,2,3,4]
输出：[2,1,4,3]
示例 2：
1
2
输入：head = []
输出：[]
示例 3：
1
2
输入：head = [1]
输出：[1]
提示：
- 链表中结点的数目在范围 [0, 100] 内
- 0 <= Node.val <= 100

思路

建议使用虚拟头结点，这样会方便很多，要不然每次针对头结点（没有前一个指针指向头结点），还要单独处理。

接下来就是交换相邻两个元素了，此时一定要画图，不画图，操作多个指针很容易乱，而且要注意操作的先后顺序：

初始时，cur指向虚拟头结点，然后进行如下三步：
![](../../../../../Running Noob/计算机/Typora笔记/笔记-git仓库/LeetCode-notebook/img/链表/两两交换链表中的结点1.png)
操作之后，链表如下：
![](../../../../../Running Noob/计算机/Typora笔记/笔记-git仓库/LeetCode-notebook/img/链表/两两交换链表中的结点2.png)

如此循环往复即可。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode swapPairs(ListNode head) {
        ListNode dummyHead = new ListNode(-1, head); //虚拟头结点
        ListNode cur, firstNode, secondNode;
        ListNode tmp;   //临时结点用来保存要交换的两个结点的再下一个结点
        cur = dummyHead;
        while (cur.next != null && cur.next.next != null) {
            firstNode = cur.next;
            secondNode = firstNode.next;
            tmp = secondNode.next;
            cur.next = secondNode;          //步骤1
            secondNode.next = firstNode;    //步骤2
            firstNode.next = tmp;           //步骤3
            cur = firstNode;
        }
        return dummyHead.next;
    }
}

5.删除链表的倒数第N个结点

题目

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。
示例 1：
1
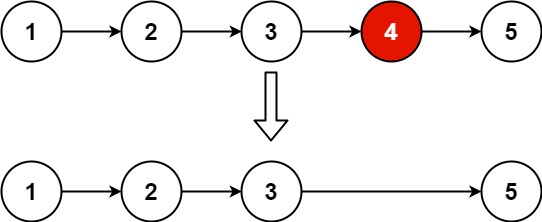
2
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]
示例 2：
1
2
输入：head = [1], n = 1
输出：[]
示例 3：
1
2
输入：head = [1,2], n = 1
输出：[1]
提示：
- 链表中结点的数目为 sz
- 1 <= sz <= 30
- 0 <= Node.val <= 100
- 1 <= n <= sz

思路

很直观的想法：先遍历一遍得到链表的长度 sz，然后从链表头结点开始向后找到第 sz-n 个结点，就是要删除的倒数第 n 个结点。

考虑到有可能删除的是倒数第 sz 个结点，即头结点，所以添加一个虚拟头结点。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        //添加虚拟头结点
        ListNode dummyHead = new ListNode(-1, head);
        ListNode pre, cur;
        //计算链表结点数
        int sz = 0;
        cur = head;
        while (cur != null) {
            sz++;
            cur = cur.next;
        }
        pre = dummyHead;
        for (int i = 0; i < sz - n; i++) {
            pre = pre.next;
        }
        cur = pre.next;	//cur指向的是要删除的结点
        pre.next = cur.next;
        return dummyHead.next;
    }
}

虚拟头结点+双指针

进阶：你能尝试使用一趟扫描实现吗？

若要使用一趟扫描实现，可以用到双指针。如果要删除倒数第 n 个结点，让 fast 移动 n 步，然后让 fast 和 slow 同时移动，直到 fast 指向链表末尾。删掉 slow 所指向的结点就可以了。

定义 fast 指针和 slow 指针，初始值为虚拟头结点，如图：
![](../../../../../Running Noob/计算机/Typora笔记/笔记-git仓库/LeetCode-notebook/img/链表/删除链表的倒数第N个结点1.png)
fast 首先走 n + 1 步，为什么是 n + 1 呢，因为只有这样同时移动的时候 slow 才能指向删除结点的上一个结点（方便做删除操作），如图：
![](../../../../../Running Noob/计算机/Typora笔记/笔记-git仓库/LeetCode-notebook/img/链表/删除链表的倒数第N个结点2.png)
让 slow 指向要删除结点的上一个结点（方便删除）。
fast 和 slow 同时移动，直到 fast 指向末尾，如图：
![](../../../../../Running Noob/计算机/Typora笔记/笔记-git仓库/LeetCode-notebook/img/链表/删除链表的倒数第N个结点3.png)
删除 slow 指向的下一个结点，如图：
![](../../../../../Running Noob/计算机/Typora笔记/笔记-git仓库/LeetCode-notebook/img/链表/删除链表的倒数第N个结点4.png)

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        //添加虚拟头结点
        ListNode dummyHead = new ListNode(-1, head);
        //快慢指针
        ListNode fastIndex, slowIndex;
        fastIndex = dummyHead;
        slowIndex = dummyHead;
        for (int i = 0; i <= n; i++) {  //让 fastIndex 向后移动 n+1 步
            fastIndex = fastIndex.next;
        }
        while (fastIndex != null) {
            fastIndex = fastIndex.next;
            slowIndex = slowIndex.next;
        }
        //此时 slowIndex 指向的是要删除结点的前一个结点
        slowIndex.next = slowIndex.next.next;
        return dummyHead.next;
    }
}

6.链表相交

题目

给你两个单链表的头结点 headA 和 headB ，请你找出并返回两个单链表相交的起始结点。如果两个链表没有交点，返回 null 。

图示两个链表在结点 c1 开始相交：

题目数据保证整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

示例 1：

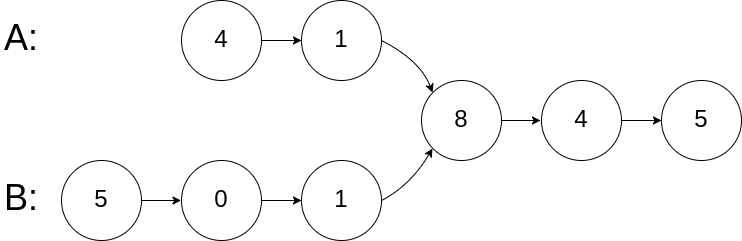
输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at '8'
解释：相交结点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。
在 A 中，相交结点前有 2 个结点；在 B 中，相交结点前有 3 个结点。

示例 2：

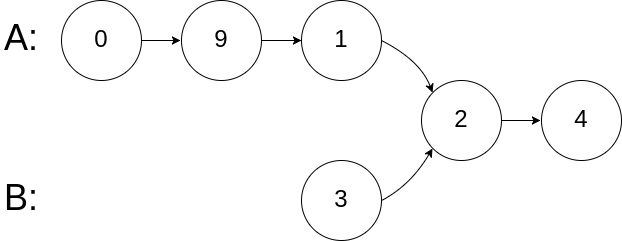
输入：intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Intersected at '2'
解释：相交结点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [0,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交结点前有 3 个结点；在 B 中，相交结点前有 1 个结点。

示例 3：

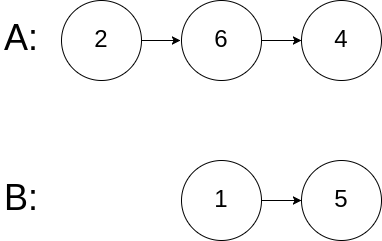
输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。

提示：

listA 中结点数目为 m
listB 中结点数目为 n
0 <= m, n <= 3 * 104
1 <= Node.val <= 105
0 <= skipA <= m
0 <= skipB <= n
如果 listA 和 listB 没有交点，intersectVal 为 0
如果 listA 和 listB 有交点，intersectVal == listA[skipA + 1] == listB[skipB + 1]

思路

简单来说，就是求两个链表交点结点的指针。这里同学们要注意，交点不是数值相等，而是指针相等。

直观的思路：对 listA 中的每一个结点，在 listB 中都遍历一遍，看看该结点是否在 listB 中，若是，则该结点就是链表相交的初始结点。

如果遍历完 listA 都没有结点在 listB 中，则这两条链表不相交。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode ANode = headA;
        ListNode BNode = headB;
        while (ANode != null) {
            while (BNode != ANode && BNode != null) {
                BNode = BNode.next;
            }
            if (BNode != null) {
                return BNode;
            }
            ANode = ANode.next;
            BNode = headB;
        }
        return null;
    }
}

时间复杂度：O(m * n)
空间复杂度：O(1)

进阶：你能否设计一个时间复杂度 O(n) 、仅用 O(1) 内存的解决方案？

如果两条链表相交，则从相交点之后两个链表的结点都是一样的、Y字形，所以直接让长链表从后面部分的结点开始和短链表进行比较，因为交点只可能出现在这段区域。如下图所示：
![](../../../../../Running Noob/计算机/Typora笔记/笔记-git仓库/LeetCode-notebook/img/链表/链表相交.png)

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode curA, curB;
        int lenA, lenB, offset;
        curA = headA;
        curB = headB;
        lenA = lenB = 0;
        //得到链表A的长度
        while (curA != null) {
            lenA++;
            curA = curA.next;
        }
        //得到链表B的长度
        while (curB != null) {
            lenB++;
            curB = curB.next;
        }
        //让curA指向长链表的头结点, curB指向短链表的头结点
        if (lenA >= lenB) {
            curA = headA;
            curB = headB;
            offset = lenA - lenB;
        }else {
            curA = headB;
            curB = headA;
            offset = lenB - lenA;
        }
        //从长链表的后面部分开始比较
        for (int i = 0; i < offset; i++) {
            curA = curA.next;
        }
        while (curA != null) {
            if (curA == curB) {
                return curA;
            }
            curA = curA.next;
            curB = curB.next;
        }
        return null;
    }
}

7.★环形链表

题目

给定一个链表的头结点 head ，返回链表开始入环的第一个结点。如果链表无环，则返回 null。
如果链表中有某个结点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1：
1
2
3
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表结点
解释：链表中有一个环，其尾部连接到第二个结点。
示例 2：
1
2
3
输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表结点
解释：链表中有一个环，其尾部连接到第一个结点。
示例 3：
1
2
3
输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。
提示：
- 链表中结点的数目范围在范围 [0, 104] 内
- -105 <= Node.val <= 105
- pos 的值为 -1 或者链表中的一个有效索引

思路

主要考察两个知识点：
- 判断链表是否有环
- 如果有环，如何找到这个环的入口

★判断链表是否有环

快慢指针法

可以使用快慢指针法，分别定义 fast 和 slow 指针，从头结点出发，fast 指针每次移动两个结点，slow 指针每次移动一个结点，如果 fast 和 slow指针在途中相遇，说明这个链表有环。
为什么 fast 走两个结点，slow 走一个结点，有环的话，一定会在环内相遇呢，而不是永远的错开呢？
- 首先第一点：fast 指针一定先进入环中，如果 fast 指针和 slow 指针相遇的话，一定是在环中相遇，这是毋庸置疑的。
- 其次，因为 fast 是走两步，slow 是走一步，其实相对于 slow 来说，fast 是一个结点一个结点的靠近 slow 的，所以 fast 一定可以和 slow 重合。

如果有环，如何找到这个环的入口

假设从头结点到环形入口结点的结点数为 x，环形入口结点到 fast 指针与 slow 指针相遇结点的结点数为 y，从相遇结点再到环形入口结点结点数为 z。如图所示：
![](../../../../../Running Noob/计算机/Typora笔记/笔记-git仓库/LeetCode-notebook/img/链表/环形链表入口.png)
- 那么相遇时： slow 指针走过的结点数为：x + y， fast 指针走过的结点数：x + y + n (y + z)，n 为 fast 指针在环内走了 n 圈才遇到 slow 指针，(y + z)为一圈内结点的个数。
- 因为 fast 指针是一步走两个结点，slow 指针一步走一个结点，所以 fast 指针走过的结点数 = slow 指针走过的结点数 * 2：(x + y) * 2 = x + y + n (y + z) ，两边消掉一个(x + y)： x + y = n (y + z) 。
  因为要找环形的入口，那么要求的是 x，因为 x 表示头结点到环形入口结点的的距离。
  所以要求 x ，将 x 单独放在左面：x = n (y + z) - y，再从 n (y + z) 中提出一个 (y + z) 来，整理公式之后为如下公式：x = (n - 1) (y + z) + z ，注意这里 n 一定是大于等于 1 的，因为 fast 指针至少要多走一圈才能相遇 slow 指针。
现在我们得到了一个公式：x = (n - 1) (y + z) + z, n >= 1。
- 以 n = 1 为例，意味着 fast 指针在环形里转了一圈之后，就遇到了 slow 指针了。
  这时公式化解为 x = z。
  这就意味着，从头结点出发一个指针，从 fast 和 slow 相遇结点处也出发一个指针，这两个指针每次只走一个结点，那么当这两个指针相遇的时候就是环形入口的结点。
  也就是在相遇结点处，定义一个指针 index1，在头结点处定一个指针 index2。让 index1 和 index2 同时移动，每次移动一个结点，那么他们相遇的地方就是环形入口的结点。
- 那么 n >= 1 是什么情况呢，就是 fast 指针在环形转 n 圈之后才遇到 slow 指针。
  其实这种情况和 n = 1 的时候的效果是一样的，一样可以通过这个方法找到环形的入口结点，只不过，index1 指针在环里多转了 (n-1) 圈，然后再遇到 index2，相遇点依然是环形的入口结点。

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode fastIndex, slowIndex;
        fastIndex = head;
        slowIndex = head;
        //得到快慢指针相遇的结点
        while (fastIndex != null && fastIndex.next != null) {
            fastIndex = fastIndex.next.next;
            slowIndex = slowIndex.next;
            if (fastIndex == slowIndex) {   //有环
                ListNode index1 = head;
                ListNode index2 = fastIndex;
                while (index1 != index2) {
                    index1 = index1.next;
                    index2 = index2.next;
                }
                return index1;
            }
        }
        return null;
    }
}

总结篇

链表的种类主要为：单链表，双链表，循环链表
链表的存储方式：链表的结点在内存中是分散存储的，通过指针连在一起。
链表是如何进行增删改查的。
数组和链表在不同场景下的性能分析。
虚拟头结点：链表的一大问题就是操作当前结点必须要找前一个结点才能操作。这就造成了，头结点的尴尬，因为头结点没有前一个结点了。
每次对应头结点的情况都要单独处理，所以使用虚拟头结点的技巧，就可以解决这个问题。
判断链表是否有环：使用快慢指针法来判断。