贪心算法Tag

贪心的本质是选择每一阶段的局部最优，从而达到全局最优。
贪心的套路（什么时候用贪心）
刷题或者面试的时候，手动模拟一下感觉可以局部最优推出整体最优，而且想不到反例，那么就试一试贪心。
贪心一般解题步骤：
贪心算法一般分为如下四步：
将问题分解为若干个子问题
找出适合的贪心策略
求解每一个子问题的最优解
将局部最优解堆叠成全局最优解

贪心算法

理论基础

贪心的本质是选择每一阶段的局部最优，从而达到全局最优。
贪心的套路（什么时候用贪心）
- 刷题或者面试的时候，手动模拟一下感觉可以局部最优推出整体最优，而且想不到反例，那么就试一试贪心。
贪心一般解题步骤：
贪心算法一般分为如下四步：
1. 将问题分解为若干个子问题
2. 找出适合的贪心策略
3. 求解每一个子问题的最优解
4. 将局部最优解堆叠成全局最优解

1.分发饼干

题目

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

示例 1:

输入: g = [1,2,3], s = [1,1]
输出: 1
解释: 
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。

示例 2:

输入: g = [1,2], s = [1,2,3]
输出: 2
解释: 
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.

提示：

1 <= g.length <= 3 * 10^4
0 <= s.length <= 3 * 10^4
1 <= g[i], s[j] <= 2^31 - 1

思路

class Solution {
    public int findContentChildren(int[] g, int[] s) {
        if (s.length == 0) { // 排除特殊情况
            return 0;
        }
        int result = 0;
        int index = 0;
        Arrays.sort(g); // 孩子们的胃口从小到大排序
        Arrays.sort(s); // 饼干的尺寸从小到大排序
        for (int i = 0; i < g.length; i++) {
            for (int j = index; j < s.length; j++) {
                if (s[j] >= g[i]) {
                    result++;
                    index = j + 1; // 只有j+1之后的饼干才能满足孩子们的胃口了
                    break;
                }
                if (j == s.length - 1) { // 剩余的饼干已经不能满足孩子们的胃口了
                    return result;
                }
            }
        }
        return result;
    }
}

2.摆动序列（贪心解法）

题目

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 摆动序列。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

例如， [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。

示例 1：

1
2
3

输入：nums = [1,7,4,9,2,5]
输出：6
解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。

示例 2：

输入：nums = [1,17,5,10,13,15,10,5,16,8]
输出：7
解释：这个序列包含几个长度为 7 摆动序列。
其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。

示例 3：

1 2	输入：nums = [1,2,3,4,5,6,7,8,9] 输出：2

提示：

1 <= nums.length <= 1000
0 <= nums[i] <= 1000

思路

本题要求通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。

来分析一下，要求删除元素使其达到最大摆动序列，应该删除什么元素呢？

用示例二来举例，如图所示：
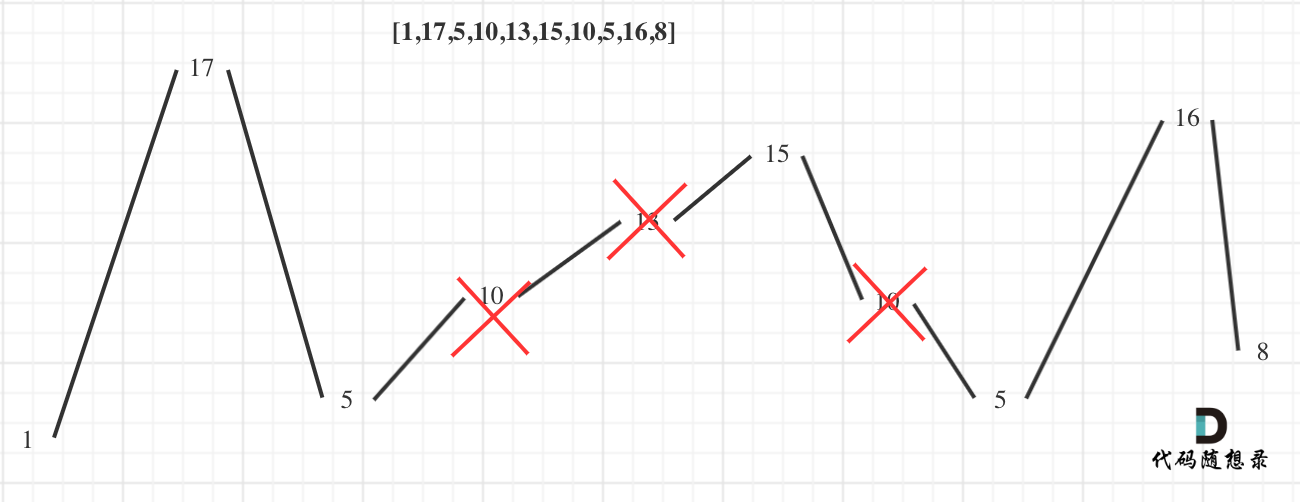
局部最优：删除单调坡度上的节点（不包括单调坡度两端的节点），那么这个坡度就可以有两个局部峰值。
整体最优：整个序列有最多的局部峰值，从而达到最长摆动序列。
- 局部最优推出全局最优，并举不出反例，那么试试贪心！
实际操作上，其实连删除的操作都不用做，因为题目要求的是最长摆动子序列的长度，所以只需要统计数组的峰值数量就可以了（相当于是删除单一坡度上的节点，然后统计长度）
这就是贪心所贪的地方，让峰值尽可能的保持峰值，然后删除单一坡度上的节点
- 在计算是否有峰值的时候，大家知道遍历的下标 i ，计算 prediff（nums[i] - nums[i-1]）和 curdiff（nums[i+1] - nums[i]），如果prediff < 0 && curdiff > 0 或者 prediff > 0 && curdiff < 0，此时就有波动需要统计。

这是我们思考本题的一个大体思路，但本题要考虑三种情况：

情况一：上下坡中有平坡
例如 [1,2,2,2,1]这样的数组，如图：
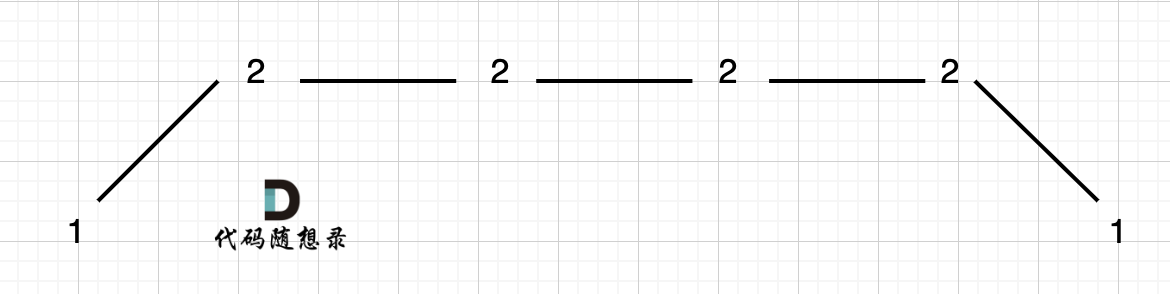
它的摇摆序列长度是多少呢？ 其实是长度是 3，也就是我们在删除的时候要不删除左面的三个 2，要不就删除右边的三个 2。
如图，可以统一规则，删除左边的三个 2：
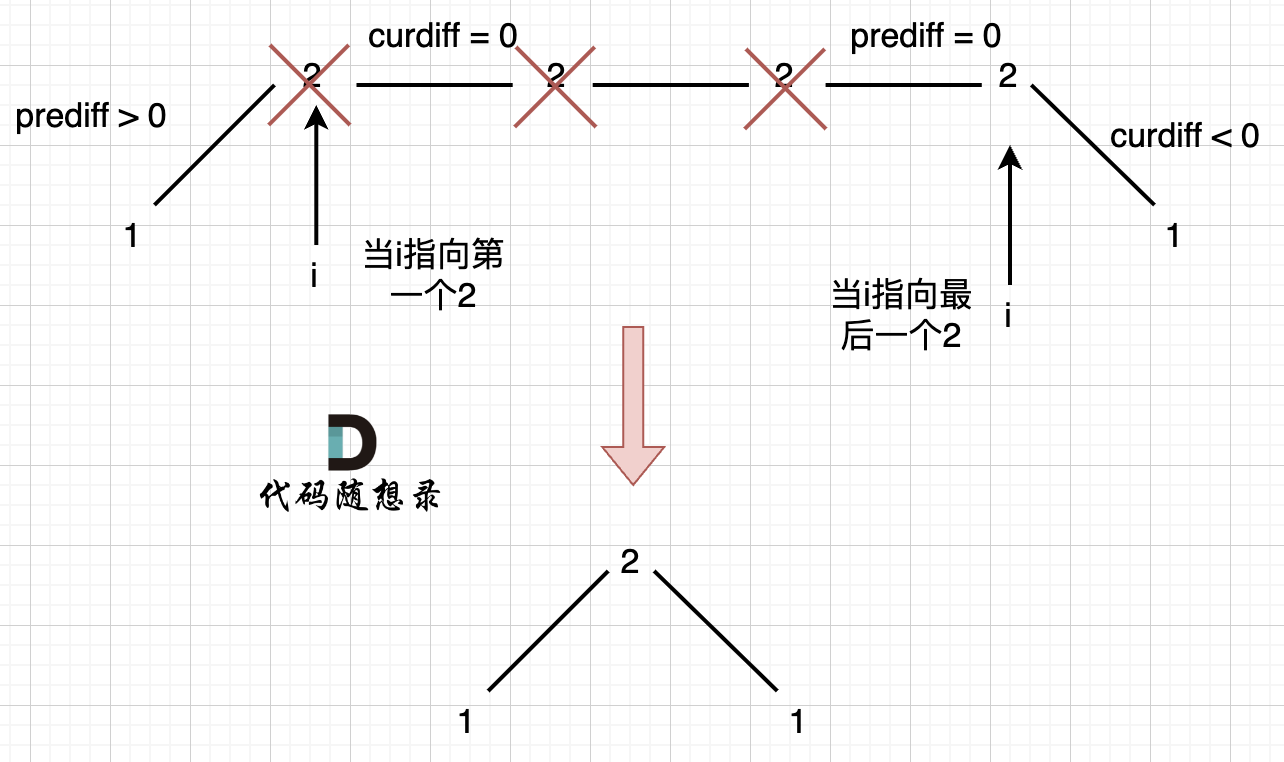
- 在图中，当 i 指向第一个 2 的时候，prediff > 0 && curdiff = 0 ，当 i 指向最后一个 2 的时候 prediff = 0 && curdiff < 0。
- 如果我们采用，删左面三个 2 的规则，那么当 prediff = 0 && curdiff < 0 也要记录一个峰值，因为他是把之前相同的元素都删掉留下的峰值。
- 所以我们记录峰值的条件应该是： (preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)，为什么这里允许 prediff = 0 ，就是上面所说的这种情况。
情况二：数组首尾两端
本题统计峰值的时候，数组最左面和最右面如何统计呢？
题目中说了，如果只有两个不同的元素，那摆动序列也是 2。例如序列[2,5]，如果靠统计差值来计算峰值个数就需要考虑数组最左面和最右面的特殊情况。
- 因为我们在计算 prediff（nums[i] - nums[i-1]）和 curdiff（nums[i+1] - nums[i]）的时候，至少需要三个数字才能计算，而数组只有两个数字。
- 这里我们可以写死，就是如果只有两个元素，且元素不同，那么结果为 2。
不写死的话，如何和我们的判断规则结合在一起呢？
- 可以假设，数组最前面还有一个数字，那这个数字应该是什么呢？
- 之前我们在讨论情况一：相同数字连续的时候， prediff = 0 ，curdiff < 0 或者 >0 也记为波谷。
  那么为了规则统一，针对序列[2,5]，可以假设为[2,2,5]，这样它就有坡度了即 preDiff = 0，如图：
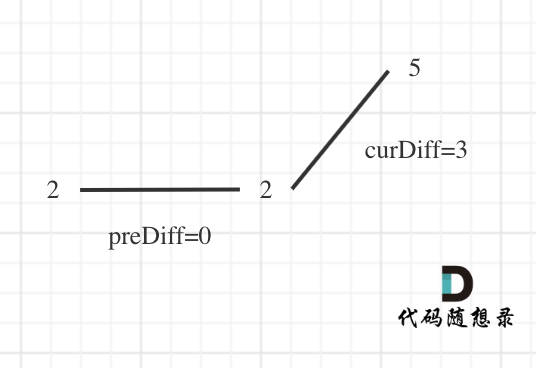
  针对以上情形，result 初始为 1（默认最右面有一个峰值），此时 curDiff > 0 && preDiff <= 0，那么 result++（计算了左面的峰值），最后得到的 result 就是 2（峰值个数为 2 即摆动序列长度为 2）

版本一的代码：

class Solution {
    public int wiggleMaxLength(int[] nums) {
        if (nums.length <= 1) { // 排除特殊情况
            return nums.length;
        }
        // preDiff记录之前的差值，curDiff记录当前的差值
        int preDiff, curDiff, result;
        preDiff = 0; // 初始时假设在nums[0]的左侧还有一个和nums[0]一样大的数
        result = 1;
        for (int i = 1; i < nums.length; i++) {
            curDiff = nums[i] - nums[i - 1];
            if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {
                result++;
            }
            preDiff = curDiff;
        }
        return result;
    }
}

情况三：单调坡中有平坡
在版本一中，我们忽略了一种情况，即如果在一个单调坡度上有平坡，例如[1,2,2,2,3,4]，如图：
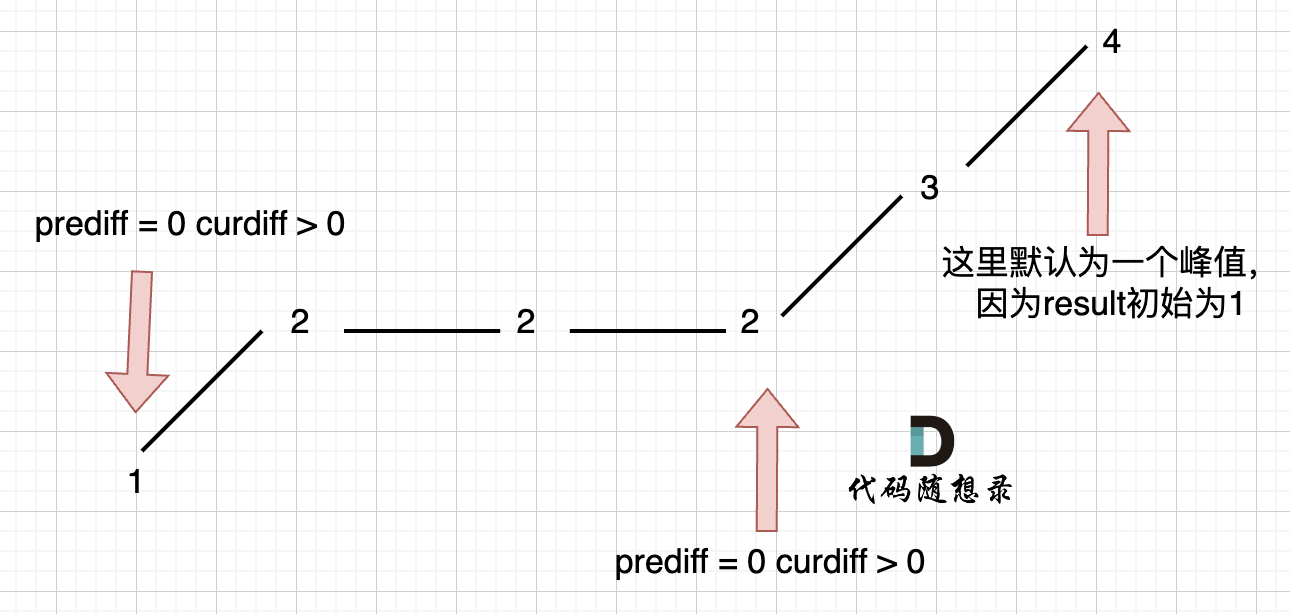
图中，我们可以看出，版本一的代码在三个地方记录峰值，但其实结果因为是 2，因为单调中的平坡不能算峰值（即摆动）。
之所以版本一会出问题，是因为我们实时更新了 prediff。
那么我们应该什么时候更新 prediff 呢？
- 我们只需要在这个坡度摆动变化的时候，更新 prediff 就行，这样 prediff 在单调区间有平坡的时候就不会发生变化，造成我们的误判。

最终的代码如下：

class Solution {
    public int wiggleMaxLength(int[] nums) {
        if (nums.length <= 1) { // 排除特殊情况
            return nums.length;
        }
        // preDiff记录之前的差值，curDiff记录当前的差值
        int preDiff, curDiff, result;
        preDiff = 0; // 初始时假设在nums[0]的左侧还有一个和nums[0]一样大的数
        result = 1;
        for (int i = 1; i < nums.length; i++) {
            curDiff = nums[i] - nums[i - 1];
            if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {
                // 只有在坡度摆动变化的时候，才更新prediff
                preDiff = curDiff;
                result++;
            }
        }
        return result;
    }
}

3.分发糖果

题目

n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。

你需要按照以下要求，给这些孩子分发糖果：

每个孩子至少分配到 1 个糖果。
相邻两个孩子评分更高的孩子会获得更多的糖果。

请你给每个孩子分发糖果，计算并返回需要准备的 最少糖果数目 。

示例 1：

1
2
3

输入：ratings = [1,0,2]
输出：5
解释：你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。

示例 2：

输入：ratings = [1,2,2]
输出：4
解释：你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
     第三个孩子只得到 1 颗糖果，这满足题面中的两个条件。

提示：

n == ratings.length
1 <= n <= 2 * 10^4
0 <= ratings[i] <= 2 * 10^4

思路

这道题目一定是要确定一边之后，再确定另一边，例如比较每一个孩子的左边，然后再比较右边，如果两边一起考虑一定会顾此失彼。

先确定右边评分大于左边的情况（也就是从前向后遍历），此时局部最优：只要右边评分比左边大，右边的孩子就多一个糖果，全局最优：相邻的孩子中，评分高的右孩子获得比左边孩子更多的糖果。
1
2
3
4
5
6
// 从前向后
for (int i = 1; i < ratings.size(); i++) {
if (ratings[i] > ratings[i - 1]){
candyNum[i] = candyNum[i - 1] + 1;
}
}
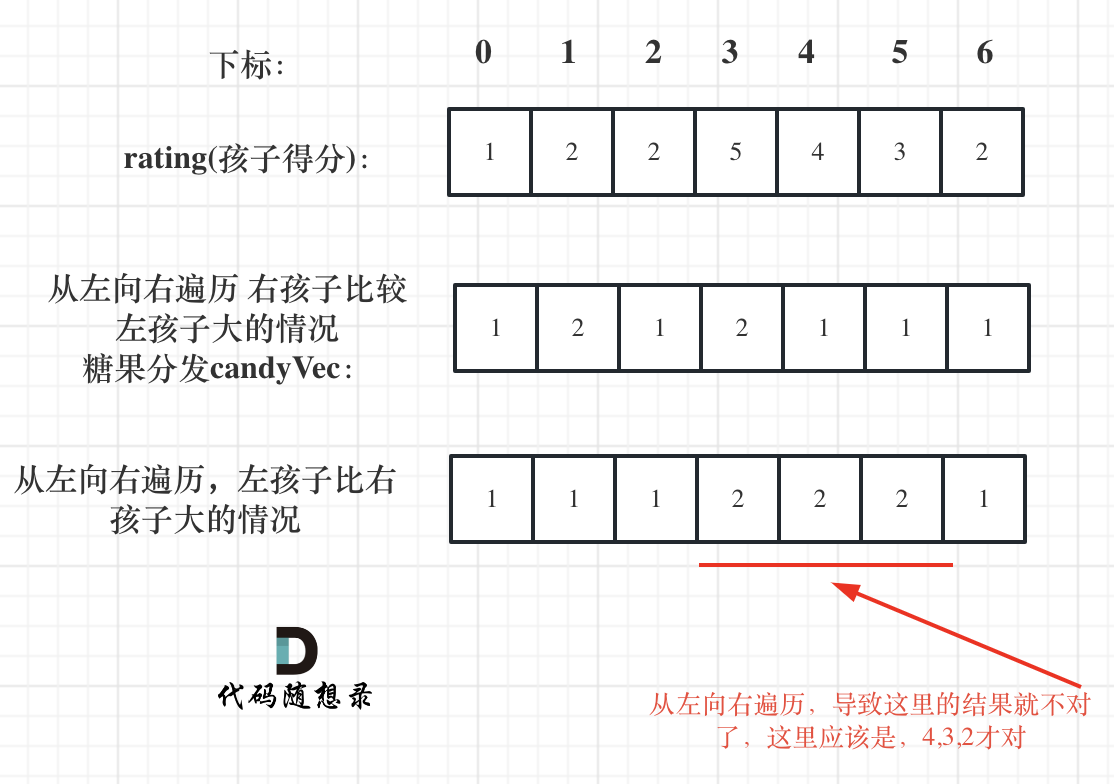
再确定左孩子大于右孩子的情况（从后向前遍历），遍历顺序这里有同学可能会有疑问，为什么不能从前向后遍历呢？
- 因为 rating[5] 与 rating[4] 的比较，要利用上 rating[5] 与 rating[6] 的比较结果，所以要从后向前遍历。如果从前向后遍历，rating[5] 与 rating[4] 的比较就不能用上 rating[5] 与 rating[6] 的比较结果了，因为从前往后遍历， rating[5] 与 rating[6] 的比较结果还没出来。
  也就是说，要先更新 rating[5] 的情况，才能正确的更新 rating[4] 的情况，否则就会出错，如图：
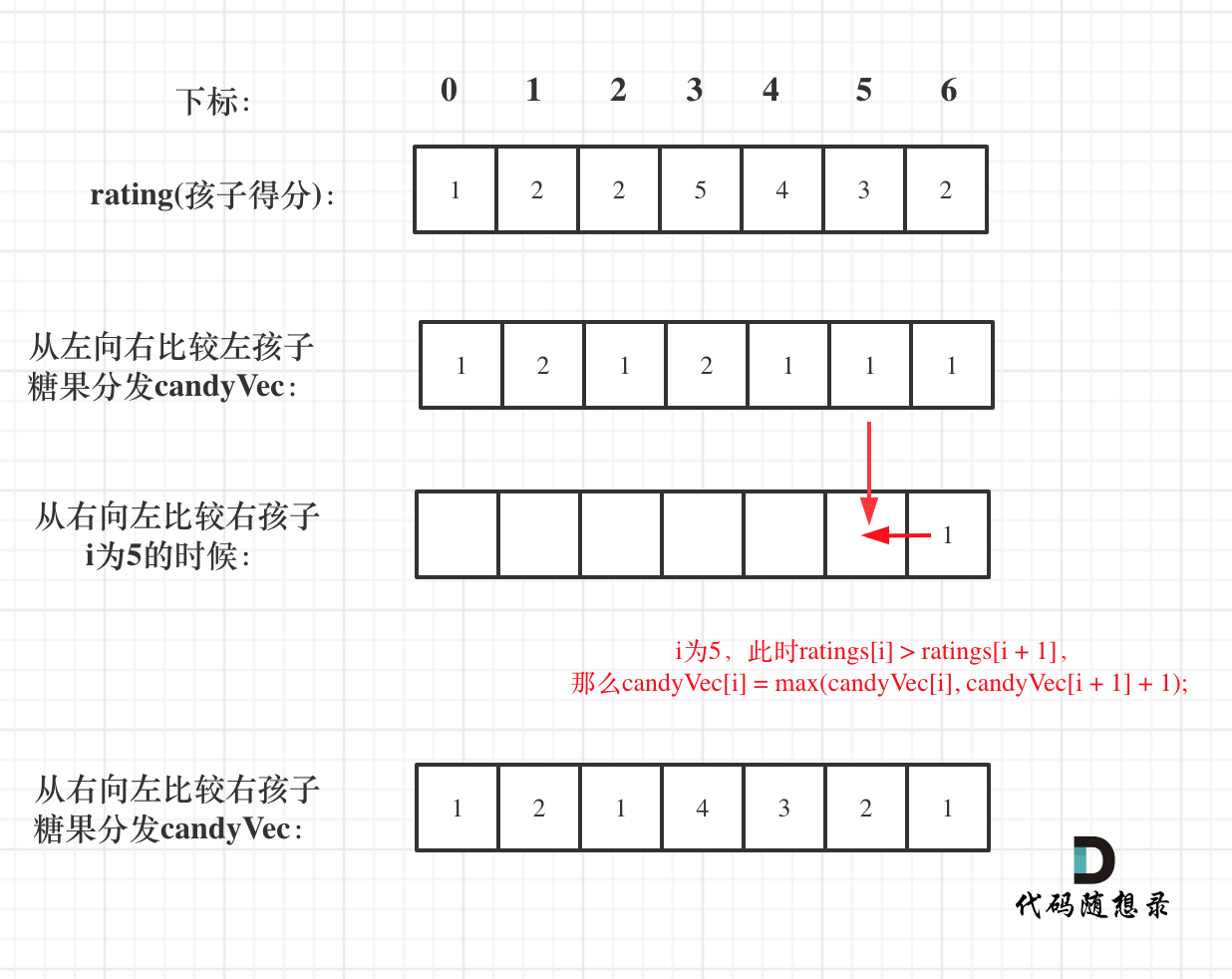
如果 ratings[i] > ratings[i + 1]，此时 candyNum[i]（第 i 个小孩的糖果数量）就有两个选择了，一个是 candyNum[i + 1] + 1（从右边这个加 1 得到的糖果数量），一个是 candyNum[i]（之前比较右孩子大于左孩子得到的糖果数量）。
- 那么又要贪心了，局部最优：取 candyNum[i + 1] + 1 和 candyNum[i] 最大的糖果数量，保证第 i 个小孩的糖果数量既大于左边的也大于右边的。全局最优：相邻的孩子中，评分高的孩子获得更多的糖果。
- 所以就取 candyNum[i + 1] + 1 和 candyNum[i] 最大的糖果数量，candyNum[i] 只有取最大的才能既保持对左边 candyNum[i - 1] 的糖果多，也比右边 candyNum[i + 1] 的糖果多。如图：

class Solution {
    public int candy(int[] ratings) {
        int result = 0;
        int[] candyNum = new int[ratings.length];
        candyNum[0] = 1;
        // 第一次遍历确定右孩子评分大于左孩子评分的情况(从前向后遍历)
        for (int i = 0; i < ratings.length - 1; i++) {
            if (ratings[i + 1] > ratings[i]) {
                candyNum[i + 1] = candyNum[i] + 1;
            } else {
                candyNum[i + 1] = 1;
            }
        }
        // 第二次遍历确定左孩子评分大于右孩子的情况(从后向前遍历)
        for (int i = ratings.length - 1; i > 0; i--) {
            if (ratings[i - 1] > ratings[i]) {
                candyNum[i - 1] = Math.max(candyNum[i - 1], candyNum[i] + 1);
            }
        }
        for (int i = 0; i < ratings.length; i++) {
            result += candyNum[i];
        }
        return result;
    }
}

4.柠檬水找零

题目

在柠檬水摊上，每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品，（按账单 bills 支付的顺序）一次购买一杯。

每位顾客只买一杯柠檬水，然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零，也就是说净交易是每位顾客向你支付 5 美元。

注意，一开始你手头没有任何零钱。

给你一个整数数组 bills ，其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零，返回 true ，否则返回 false 。

示例 1：

输入：bills = [5,5,5,10,20]
输出：true
解释：
前 3 位顾客那里，我们按顺序收取 3 张 5 美元的钞票。
第 4 位顾客那里，我们收取一张 10 美元的钞票，并返还 5 美元。
第 5 位顾客那里，我们找还一张 10 美元的钞票和一张 5 美元的钞票。
由于所有客户都得到了正确的找零，所以我们输出 true。

示例 2：

输入：bills = [5,5,10,10,20]
输出：false
解释：
前 2 位顾客那里，我们按顺序收取 2 张 5 美元的钞票。
对于接下来的 2 位顾客，我们收取一张 10 美元的钞票，然后返还 5 美元。
对于最后一位顾客，我们无法退回 15 美元，因为我们现在只有两张 10 美元的钞票。
由于不是每位顾客都得到了正确的找零，所以答案是 false。

提示：

1 <= bills.length <= 10^5
bills[i] 不是 5 就是 10 或是 20

思路

只需要维护三种金额的数量，5，10和20。

有如下三种情况：

情况一：账单是 5，直接收下。
情况二：账单是 10，消耗一个 5，增加一个 10
情况三：账单是 20，优先消耗一个 10 和一个 5，如果不够，再消耗三个 5。
- 在情况三，优先消耗 10 美元的策略，就体现了贪心，因为 5 美元相比 10 美元更适用。

class Solution {
    public boolean lemonadeChange(int[] bills) {
        int fiveNum, tenNum, twentyNum;
        fiveNum = tenNum = twentyNum = 0;
        for (int i = 0; i < bills.length; i++) {
            // 先假设找零充足
            if (bills[i] == 5) {
                fiveNum++; // 得到一张5美元
            } else if (bills[i] == 10) {
                tenNum++; // 得到一张10美元
                fiveNum--; // 找零一张5美元
            } else if (bills[i] == 20) {
                // 先假设直接找零一张10美元和一张5美元
                twentyNum++; // 得到一张二十美元
                tenNum--; // 找零一张10美元
                fiveNum--; // 找零一张5美元
            }
            // 如果10美元不够，再用5美元来补
            if (tenNum == -1) {
                tenNum++;
                fiveNum -= 2;
            }
            // 再判断是否出现找零不够的情况
            if (fiveNum < 0) {
                return false;
            }
        }
        return true;
    }
}