动态规划Tag

动态规划的解题步骤：
确定dp数组（dp table）以及下标的含义
确定递推公式
dp 数组如何初始化
确定遍历顺序
举例推导 dp 数组

动态规划

理论基础

动态规划，英文：Dynamic Programming，简称 DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。
- 动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有状态推导，而是从局部直接选最优的。
  大家知道动规是由前一个状态推导出来的，而贪心是局部直接选最优的，对于刷题来说就够用了。

★动归五部曲

动态规划的解题步骤：
1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp 数组如何初始化
4. 确定遍历顺序
5. 举例推导 dp 数组
- 状态转移公式（递推公式）是很重要，但动规不仅仅只有递推公式。
  对于动态规划问题，上面这五步都搞清楚了，才能说把动态规划真的掌握了。
一些同学可能想为什么要先确定递推公式，然后在考虑初始化呢？
- 因为一些情况是递推公式决定了 dp 数组要如何初始化。
动态规划应该如何 debug？
- 找问题的最好方式就是把dp数组打印出来，看看究竟是不是按照自己思路推导的！
- 一些同学对于 dp 的学习是黑盒的状态，就是不清楚 dp 数组的含义，不懂为什么这么初始化，递推公式背下来了，遍历顺序靠习惯就是这么写的，然后一鼓作气写出代码，如果代码能通过万事大吉，通过不了的话就凭感觉改一改。
  - 这是一个很不好的习惯！
- 做动规的题目，写代码之前一定要把状态转移在 dp 数组的上具体情况模拟一遍，心中有数，确定最后推出的是想要的结果。然后再写代码，如果代码没通过就打印 dp 数组，看看是不是和自己预先推导的哪里不一样。如果打印出来和自己预先模拟推导是一样的，那么就是自己的递归公式、初始化或者遍历顺序有问题了。如果和自己预先模拟推导的不一样，那么就是代码实现细节有问题。
  - 这样才是一个完整的思考过程，而不是一旦代码出问题，就毫无头绪的东改改西改改，最后过不了，或者说是稀里糊涂的过了。

1.摆动序列（动态规划）

题目

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 摆动序列。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

例如， [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。

示例 1：

1
2
3

输入：nums = [1,7,4,9,2,5]
输出：6
解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。

示例 2：

输入：nums = [1,17,5,10,13,15,10,5,16,8]
输出：7
解释：这个序列包含几个长度为 7 摆动序列。
其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。

示例 3：

1 2	输入：nums = [1,2,3,4,5,6,7,8,9] 输出：2

提示：

1 <= nums.length <= 1000
0 <= nums[i] <= 1000

思路

很容易可以发现，对于我们当前考虑的这个数，要么是作为山峰（即 nums[i] > nums[i-1]），要么是作为山谷（即 nums[i] < nums[i - 1]）。

设 dp 状态dp[i][0]，表示考虑前 i 个数，第 i 个数作为山峰的摆动子序列的最长长度
设 dp 状态dp[i][1]，表示考虑前 i 个数，第 i 个数作为山谷的摆动子序列的最长长度

则转移方程为：

dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + 1), nums[i] > nums[i - 1]，表示将 nums[i] 接到前面某个山谷后面，作为山峰。
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + 1), nums[i] < nums[i - 1]，表示将 nums[i] 接到前面某个山峰后面，作为山谷。
如果 nums[i] == nums[i - 1]，则直接继承之前的值即可：
- dp[i][0] = dp[i - 1][0]
- dp[i][1] = dp[i - 1][1]

初始状态：

dp[0][0] = dp[0][1] = 1。

class Solution {
    public int wiggleMaxLength(int[] nums) {
        int[][] dp = new int[nums.length][2];
        // 递推表达式：
        // dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + 1), nums[i] > nums[i - 1]
        // dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + 1), nums[i] < nums[i - 1]
        // 初始化
        dp[0][0] = dp[0][1] = 1;
        // 遍历
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] == nums[i - 1]) {
                dp[i][0] = dp[i - 1][0];
                dp[i][1] = dp[i - 1][1];
            }
            // i是波峰
            if (nums[i] > nums[i - 1]) {
                dp[i][0] = Math.max(dp[i][0], dp[i - 1][1] + 1);
                dp[i][1] = dp[i - 1][1];
            }
            // i是波谷
            if (nums[i] < nums[i - 1]) {
                dp[i][1] = Math.max(dp[i][1], dp[i - 1][0] + 1);
                dp[i][0] = dp[i - 1][0];
            }
        }
        return Math.max(dp[nums.length - 1][0], dp[nums.length - 1][1]);
    }
}

2.斐波那契数

题目

斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

1 2	F(0) = 0，F(1) = 1 F(n) = F(n - 1) + F(n - 2)，其中 n > 1

给定 n ，请计算 F(n) 。

示例 1：

1
2
3

输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2：

1
2
3

输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2

示例 3：

1
2
3

输入：n = 4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3

提示：

0 <= n <= 30

思路

这道题目比较简单，可能一些同学并不需要做什么分析，直接顺手一写就过了。但「代码随想录」的风格是：简单题目是用来加深对解题方法论的理解的。通过这道题目让大家可以初步认识到，按照动规五部曲是如何解题的。
- 对于动规，如果没有方法论的话，可能简单题目可以顺手一写就过，难一点就不知道如何下手了。

动规五部曲：

确定 dp 数组以及下标的含义：
- dp[i] 的定义为：第 i 个数的斐波那契数值是 dp[i]
确定递推公式：
- 题目已经把递推公式直接给我们了：状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];
dp 数组如何初始化：
- 题目中把如何初始化也直接给我们了，如下：
  1
  2
  dp[0] = 0;
  dp[1] = 1;
确定遍历顺序：
- 从递归公式 dp[i] = dp[i - 1] + dp[i - 2]; 中可以看出，dp[i] 是依赖 dp[i - 1] 和 dp[i - 2] 的，那么遍历的顺序一定是从前到后遍历的。
举例推导 dp 数组：
- 按照这个递推公式 dp[i] = dp[i - 1] + dp[i - 2]，我们来推导一下，当 N 为 10 的时候，dp 数组应该是如下的数列：
  1
  0 1 1 2 3 5 8 13 21 34 55
  如果代码写出来，发现结果不对，就把 dp 数组打印出来看看和我们推导的数列是不是一致的。

class Solution {
    public int fib(int n) {
        if (n < 2) { // 排除特殊情况
            return n;
        }
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

3.爬楼梯

题目

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

提示：

1 <= n <= 45

思路

爬到第一层楼梯有一种方法，爬到二层楼梯有两种方法。
- 那么第一层楼梯再跨两步就到第三层，第二层楼梯再跨一步就到第三层。
  所以到第三层楼梯的状态可以由第二层楼梯和到第一层楼梯状态推导出来，那么就可以想到动态规划了。

我们来分析一下，动规五部曲：

确定 dp 数组以及下标的含义：
- dp[i]：爬到第 i 层楼梯，有 dp[i] 种方法
确定递推公式：
- 从 dp[i] 的定义可以看出，dp[i] 可以有两个方向推出来。
  - 首先是 dp[i - 1]，上 i-1 层楼梯，有 dp[i - 1] 种方法，那么再一步跳一个台阶不就是 dp[i] 了么。
  - 还有就是 dp[i - 2]，上 i-2 层楼梯，有 dp[i - 2] 种方法，那么再一步跳两个台阶不就是 dp[i] 了么。
  那么 dp[i] 就是 dp[i - 1] 与 dp[i - 2] 之和：dp[i] = dp[i - 1] + dp[i - 2]
dp 数组如何初始化：
- 不考虑 dp[0] 如何初始化，只初始化 dp[1] = 1，dp[2] = 2，然后从 i = 3 开始递推。
确定遍历顺序：
- 从递推公式 dp[i] = dp[i - 1] + dp[i - 2]; 中可以看出，遍历顺序一定是从前向后遍历的。
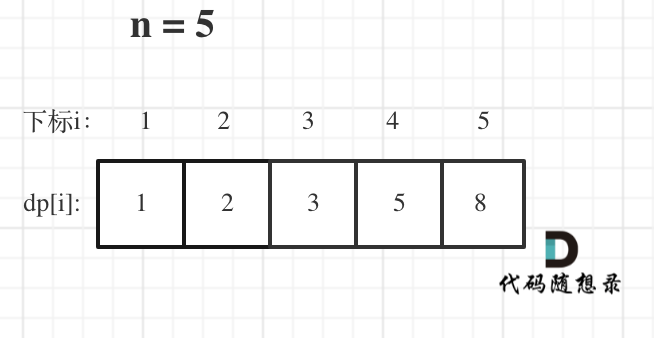
举例推导 dp 数组：
- 举例当 n 为 5 的时候，dp table（dp 数组）应该是这样的：

class Solution {
    public int climbStairs(int n) {
        if (n <= 1) { // 排除特殊情况
            return n;
        }
        int[] dp = new int[n + 1];
        // dp[i]：爬到第i层楼梯的方法次数
        // 递推公式：dp[i] = dp[i - 2] + dp[i - 1]
        // 初始化
        dp[1] = 1;
        dp[2] = 2;
        // 遍历
        for (int i = 3; i < n + 1; i++) {
            dp[i] = dp[i - 2] + dp[i - 1];
        }
        return dp[n];
    }
}

这题用回溯也能做，而且不止针对一次只能爬一层楼梯或者两层楼梯，就算一次爬 m 层楼梯，也可以求解，但是回溯法在 LeetCode 中执行超时了（就算已经剪枝了）：

class Solution {
    private int result = 0;
    private int[] steps = {1, 2};
    public int climbStairs(int n) {
        backTracking(n, 0);
        return result;
    }

    // climb是已经爬的阶数
    public boolean backTracking(int n, int climb) {
        if (climb > n) {
            return false;
        }
        if (climb == n) {
            result++;
            return true;
        }
        for (int i = 0; i < steps.length; i++) {
            climb += steps[i];
            boolean isEnd = backTracking(n, climb);
            climb -= steps[i]; // 回溯
            // 如果当前step已经能到楼顶，那后面步伐更大的step就不需要遍历了
            if (isEnd) { // 剪枝
                break;
            }
        }
        return false;
    }
}