- dfs 是往一个方向去搜,不到黄河不回头,直到遇到绝境了,搜不下去了,再换方向(换方向的过程就涉及到了回溯)。
- bfs 是先把本结点所连接的所有结点遍历一遍,走到下一个结点的时候,再把连接结点所连接的所有结点遍历一遍,搜索方向更像是广度,四面八方的搜索过程。
图论
深度优先搜索理论基础
- dfs 是往一个方向去搜,不到黄河不回头,直到遇到绝境了,搜不下去了,再换方向(换方向的过程就涉及到了回溯)。
★DFS代码框架(递归+回溯)
因为 dfs 搜索往一个方向,并需要回溯,所以用递归的方式来实现是最方便的。
1
2
3
4
5
6
7
8
9
10
11
12void dfs(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本结点所连接的其他结点) {
处理结点;
dfs(图,选择的结点); // 递归
回溯,撤销处理结果
}
}- 可以发现 dfs 的代码框架和回溯算法的代码框架是差不多的。
深搜三部曲如下:
确认递归函数,参数。
通常我们递归的时候,我们递归搜索需要了解哪些参数,其实也可以在写递归函数的时候,发现需要什么参数,再去补充就可以。一般情况,深搜需要 二维数组结构保存所有路径,需要一维数组保存单一路径,这种保存结果的数组,我们可以定义一个全局变量,避免让我们的函数参数过多。例如这样:
1
2
3List<List<int>> result; // 保存符合条件的所有路径
List<int> path; // 起点到终点的路径
void dfs (图,目前搜索的结点)确认终止条件。
终止条件很重要,很多同学写 dfs 的时候,之所以容易死循环,栈溢出等等这些问题,都是因为终止条件没有想清楚。
终止不仅是结束本层递归的时候,同时也是我们收获结果的时候。
1
2
3
4if (终止条件) {
存放结果;
return;
}处理目前搜索结点出发的路径。
一般这里就是一个 for 循环的操作,去遍历目前搜索结点所能到的所有结点。
1
2
3
4
5for (选择:本结点所连接的其他结点) {
处理结点;
dfs(图,选择的结点); // 递归
回溯,撤销处理结果
}
广度优先搜索理论基础
- bfs 是先把本结点所连接的所有结点遍历一遍,走到下一个结点的时候,再把连接结点所连接的所有结点遍历一遍,搜索方向更像是广度,四面八方的搜索过程。
★BFS代码框架(队列)
我们需要一个容器,能保存我们要遍历过的元素,用队列,用栈,甚至用数组,都是可以的。
- 用队列的话,就是保证每一圈都是一个方向去转,例如统一顺时针或者逆时针。
- 如果用栈的话,就是第一圈顺时针遍历,第二圈逆时针遍历,第三圈有顺时针遍历。
那么广搜需要注意转圈搜索的顺序吗? 不需要!
所以用队列,还是用栈都是可以的,但大家都习惯用队列了,所以后面都用队列来实现。
1
2
3
4
5
6
7
8
9
10
11void bfs(参数) {
Queue<?> queue = new LinkedList<>();
queue.offer(结点);
while (!queue.isEmpty()) {
结点 = queue.poll();
for (结点:本结点所连接的其他结点) {
处理结点;
queue.offer(结点);
}
}
}
1.所有可能的路径
题目
给你一个有
n个结点的 有向无环图(DAG),请你找出所有从结点0到结点n-1的路径并输出(不要求按特定顺序)graph[i]是一个从结点i可以访问的所有结点的列表(即从结点i到结点graph[i][j]存在一条有向边)。示例 1:

1
2
3输入:graph = [[1,2],[3],[3],[]]
输出:[[0,1,3],[0,2,3]]
解释:有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3示例 2:

1
2输入:graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出:[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]提示:
n == graph.length2 <= n <= 150 <= graph[i][j] < ngraph[i][j] != i(即不存在自环)graph[i]中的所有元素 互不相同- 保证输入为 有向无环图(DAG)
思路
使用深搜三部曲来分析题目:
确认递归函数,参数:
- 首先我们 dfs 函数一定要存一个图,用来遍历的,还要存一个目前我们遍历的结点,定义为 x。至于单一路径,和路径集合则可以放在全局变量,那么代码是这样的:
1
2
3
4
5List<List<Integer>> result; // 收集符合条件的路径
List<Integer> path; // 0结点到终点的路径
// node:目前遍历的结点
// graph:存当前的图
void dfs (int[][] graph, int node)确认终止条件:
- 什么时候我们就找到一条路径了?-> 当目前遍历的结点为最后一个结点的时候,就找到了一条从出发点到终止点的路径。
- 当前遍历的结点,我们定义为 node,最后一点结点,就是
graph.size() - 1(因为题目描述是找出所有从结点 0 到结点 n-1 的路径并输出)。所以当 node 等于graph.size() - 1的时候就找到一条有效路径。 代码如下:
1
2
3
4
5// 要求从结点 0 到结点 n-1 的路径并输出,所以是 graph.size() - 1
if (node == graph.size() - 1) { // 找到符合条件的一条路径
result.add(new ArrayList<>(path)); // 收集有效路径
return;
}处理目前搜索结点出发的路径:
- 接下来是走当前遍历结点 node 的下一个结点。
- 首先是要找到 node 结点连接了哪些结点,然后就是将选中的 node 所连接的结点加入到单一路径中来,最后就是回溯的过程,撤销本次添加结点的操作。代码如下:
1
2
3
4
5
6int[] array = graph[node];
for (int i = 0; i < array.length; i++) { // 遍历结点n链接的所有结点
path.add(graph[node][i]); // 遍历到的结点加入到路径中来
dfs(graph, graph[node][i]); // 进入下一层递归
path.remove(path.size() - 1); // 回溯,撤销本结点
}
最后整体代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
private List<List<Integer>> result = new ArrayList<>();
private List<Integer> path = new ArrayList<>();
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
path.add(0);
dfs(graph, 0);
return result;
}
public void dfs(int[][] graph, int node) {
if (node == graph.length - 1) {
result.add(new ArrayList<>(path));
return;
}
int[] array = graph[node];
for (int i = 0; i < array.length; i++) {
path.add(array[i]);
dfs(graph, array[i]);
path.remove(path.size() - 1); // 回溯
}
}
}
2.岛屿数量(dfs)
题目
给你一个由
'1'(陆地)和'0'(水)组成的的二维网格,请你计算网格中岛屿的数量。岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
1
2
3
4
5
6
7输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1示例 2:
1
2
3
4
5
6
7输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 300grid[i][j]的值为'0'或'1'
思路
注意题目中每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:

这道题题目是 DFS,BFS,并查集,基础题目。
本题思路,是用遇到一个没有遍历过的结点陆地,计数器就加一,然后把该结点陆地所能遍历到的陆地都标记上。
在遇到标记过的陆地结点和海洋结点的时候直接跳过。 这样计数器就是最终岛屿的数量。
那么如何把结点陆地所能遍历到的陆地都标记上呢,就可以使用 DFS,BFS或者并查集。
DFS 解法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40class Solution {
private int[][] dir = {
{0, 1}, // 右
{1, 0}, // 下
{0, -1}, // 左
{-1, 0} // 上
};
public int numIslands(char[][] grid) {
int result = 0;
// 用于判断是否遍历过
boolean[][] isVisited = new boolean[grid.length][grid[0].length];
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
// 遇到还没遍历过的陆地
if (!isVisited[i][j] && grid[i][j] == '1') {
result++;
// 将陆地和与之相连的陆地都遍历过去
dfs(grid, isVisited, i, j);
}
}
}
return result;
}
public void dfs(char[][] grid, boolean[][] isVisited, int x, int y) {
if (isVisited[x][y] || grid[x][y] == '0') {
return;
}
isVisited[x][y] = true;
// 遍历四个方向
for (int i = 0; i < 4; i++) {
int nextX = x + dir[i][0];
int nextY = y + dir[i][1];
if (nextX < 0 || nextX >= grid.length || nextY < 0 || nextY >= grid[0].length) {
continue;
}
dfs(grid, isVisited, nextX, nextY);
}
}
}因为上面创建了一个
isVisited数组,所以执行时间会更久一点,其实我们完全可以根据grid本身来判断是否遍历过陆地:为了统计岛屿数量同时不重复记录,每当我们搜索到一个岛后,就将这个岛 “淹没” —— 将这个岛所占的地方从 “1” 改为 “0”,这样就不用担心后续会重复记录这个岛屿了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution {
public int numIslands(char[][] grid) {
int result = 0;
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
// 遇到还没遍历过的陆地
if (grid[i][j] == '1') {
result++;
// 将陆地和与之相连的陆地都遍历过去
dfs(grid, i, j);
}
}
}
return result;
}
public void dfs(char[][] grid, int x, int y) {
if (x < 0 || x >= grid.length || y < 0 || y >= grid[0].length || grid[x][y] == '0') {
return;
}
grid[x][y] = '0'; // 淹没
dfs(grid, x - 1, y); // 上
dfs(grid, x, y + 1); // 右
dfs(grid, x + 1, y); // 下
dfs(grid, x, y - 1); // 左
}
}
3.岛屿数量(bfs)
题目
给你一个由
'1'(陆地)和'0'(水)组成的的二维网格,请你计算网格中岛屿的数量。岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
1
2
3
4
5
6
7输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1示例 2:
1
2
3
4
5
6
7输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 300grid[i][j]的值为'0'或'1'
思路
BFS 解法:
这里有一个广搜中很重要的细节:只要加入队列就代表走过,就需要标记,而不是从队列拿出来的时候再去标记走过。
很多同学可能感觉这有区别吗?如果从队列拿出结点,再去标记这个结点走过,就会发生下图所示的结果,会导致很多结点重复加入队列。
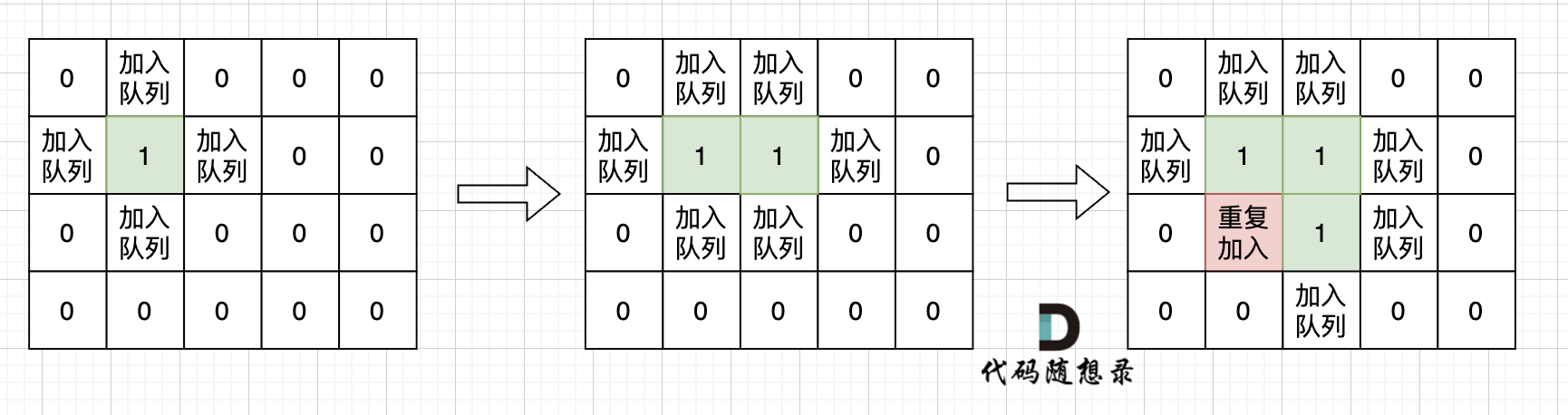
BFS 代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41class Solution {
private int[][] dir = {
{-1, 0}, // 上
{0, 1}, // 右
{1, 0}, // 下
{0, -1} // 左
};
public int numIslands(char[][] grid) {
int result = 0;
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == '1') {
result++;
bfs(grid, i, j);
}
}
}
return result;
}
public void bfs(char[][] grid, int x, int y) {
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[]{x, y});
grid[x][y] = '0'; // 淹没
while (!queue.isEmpty()) {
int[] loc = queue.poll();
int m = loc[0];
int n = loc[1];
for (int i = 0; i < 4; i++) {
int nextX = m + dir[i][0];
int nextY = n + dir[i][1];
if (nextX < 0 || nextX >= grid.length || nextY < 0 || nextY >= grid[0].length || grid[nextX][nextY] == '0') {
continue;
}
// 将与之连接的陆地也淹没
queue.offer(new int[]{nextX, nextY});
grid[nextX][nextY] = '0';
}
}
}
}