- 小红的区间翻转
- 两个字符串的最小 ASCII 删除总和
- 最长同值路径
1.小红的区间翻转
时间限制:1.000S 空间限制:256MB
题目描述
小红拿到了两个长度为 n 的数组 a 和 b,她仅可以执行一次以下翻转操作:选择a数组中的一个区间[i, j],(i != j),将它们翻转。例如,对于 a = [2,3,4,1,5,6],小红可以选择左闭右闭区间[2,4],数组 a 则变成[2,3,5,1,4,6]。
小红希望操作后 a 数组和 b 数组完全相同。请你告诉小红有多少种操作的方案数。
初始 a 数组和 b 数组必定不相同。
输入描述
第一行输入一个正整数 n,代表数组的长度;
第二行输入 n 个正整数 ai;
第三行输入 n 个正整数 bi。
输出描述
选择区间的方案数。
输入示例
输出示例
提示信息
数据范围
1 ≤ n, ai ,bi ≤ 103
在示例中:
将 1 2 3 1 中的 2 3 进行翻转,得到 1 3 2 1。
将 1 2 3 1 整个进行翻转,得到 1 3 2 1。
所以最终结果是 2。
题解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[] a = new int[n];
int[] b = new int[n];
for (int i = 0; i < n; i++) {
a[i] = in.nextInt();
}
for (int i = 0; i < n; i++) {
b[i] = in.nextInt();
}
int res = getSolutions(a, b, n);
System.out.println(res);
}
public static int getSolutions(int[] a, int[] b, int n) {
int left = 0;
int right = n - 1;
int count = 0;
while (left < n && a[left] == b[left]) {
left++;
}
while (right >= 0 && a[right] == b[right]) {
right--;
}
if (!isReverse(a, b, left, right)) {
return 0;
}
while (left >= 0 && right < n && a[left] == b[right]) {
count++;
left--;
right++;
}
return count;
}
public static boolean isReverse(int[] a, int[] b, int left, int right) {
while (left <= right && a[left] == b[right]) {
left++;
right--;
}
return left > right;
}
}
|
2.两个字符串的最小 ASCII 删除总和
时间限制:1.000S 空间限制:256MB
题目描述
给定两个字符串 s1 和 s2(0 <= s1.length, s2.length <= 1000),返回使两个字符用相等所需删除字符的 ASCLL 值的最小和。
s1 和 s2 由小写英文字母组成。
输入描述
输入共两行,每行一个字符串。
输出描述
输出一个正整数,表示使两个字符用相等所需删除字符的 ASCLL 值的最小和。
输入示例
输出示例
提示信息
解释:在“sea”中删除“s”并将”s”的值(115)加入总和。
在”eat”中删除“t“并将116 加入总和。
结束时,两个字符串相等,115+116 =231 就是符合条件的很小和。
题解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String s1 = in.nextLine();
String s2 = in.nextLine();
int m = s1.length();
int n = s2.length();
int[][] dp = new int[m + 1][n + 1];
dp[0][0] = 0;
for (int i = 1; i <= m; i++) {
dp[i][0] = dp[i - 1][0] + s1.charAt(i - 1);
}
for (int j = 1; j <= n; j++) {
dp[0][j] = dp[0][j - 1] + s2.charAt(j - 1);
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1];
}else {
dp[i][j] = Math.min(dp[i - 1][j] + s1.charAt(i - 1),
dp[i][j - 1] + s2.charAt(j - 1));
}
}
}
System.out.println(dp[m][n]);
}
}
|
3.最长同值路径
题目
题目描述
给定一个二叉树的 root ,返回最长的路径的长度,这个路径中的每节点具有相同值。这条路径可以经过也可以不经过根节点。两个节点之间的路径长度 由它们之间的边数表示。
树的节点数的范围是 [0,10^4] -1000 <= Node.val <= 1000
树的深度将不超过 18 层
输入描述
输入共两行,第一行是一个整数 n,表示第二行的字符串数。
第二行包含 n 个字符串,空格隔开,数字的字符串代表该节点存在,并且值为数字,null 代表是一个空结点。
输出描述
输出一个正整数,代表最长路径长度。
输入示例
输出示例
提示信息
通过层序遍历构建二叉树如下:
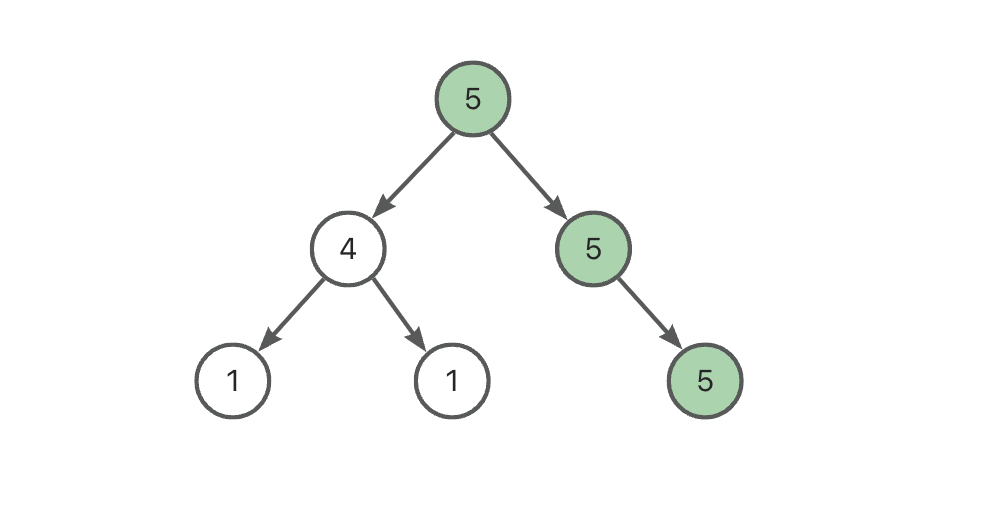
思路
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
| import java.util.Scanner;
import java.util.Queue;
import java.util.LinkedList;
public class Main{
private static int res = 0;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
if (n <= 1) {
System.out.println(0);
return;
}
in.nextLine();
String data = in.nextLine();
TreeNode root = deserialize(data, n);
dfs(root);
System.out.println(res);
}
public static int dfs(TreeNode node) {
if (node == null) {
return 0;
}
int lcur = dfs(node.left);
int rcur = dfs(node.right);
int cur = 0;
int max = 0;
if (node.left != null && node.left.val == node.val) {
cur = lcur + 1;
max += (lcur + 1);
}
if (node.right != null && node.right.val == node.val) {
cur = Math.max(cur, rcur + 1);
max += (rcur + 1);
}
res = Math.max(res, max);
return cur;
}
public static TreeNode deserialize(String data, int n) {
String[] vals = data.split(" ");
TreeNode root = new TreeNode(Integer.parseInt(vals[0]));
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int i = 1;
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
if (!vals[i].equals("null")) {
node.left = new TreeNode(Integer.parseInt(vals[i]));
queue.offer(node.left);
}
i++;
if (i >= n) {
break;
}
if (!vals[i].equals("null")) {
node.right = new TreeNode(Integer.parseInt(vals[i]));
queue.offer(node.right);
}
i++;
if (i >= n) {
break;
}
}
return root;
}
}
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) {
this.val = val;
}
}
|
