前缀和Tag

前缀和算法是一种用于高效计算数组前缀和的算法。前缀和是指从数组的起始位置到某一位置的所有元素的和。

前缀和

★理论基础

前缀和算法是一种用于高效计算数组前缀和的算法。前缀和是指从数组的起始位置到某一位置的所有元素的和。
如下图：绿色区域的和就是前缀和数组中的 S[6]。
- 这里我们需要注意的是：前 6 个数的和是 S[6]，但是数组第 6 个数下标不应该是 5 吗？
  - 我们在下表面推导公式会讲到这个问题。
前缀和算法其实是一个小的动态规划，其算法一般步骤如下：
1. 创建一个比原始数组长度长 1 的前缀和数组。
2. 遍历原始数组，计算每个位置处的前缀和，即将前一个位置的前缀和与当前位置的元素相加。
3. 将计算得到的前缀和存储到前缀和数组的相应位置。
4. 完成遍历后，前缀和数组中存储了原始数组每个位置的前缀和值。
代码步骤：
1. 先定义⼀个前缀和数组：用 dp[i] 表示第 1 项到第 i 项区间内所有元素的和（后面会发现，第 1 项到第 i 项区间内所有元素的和就是 dp[i] - dp[0]，但是 dp[0] 初始化为 0，所以就是 dp[i]），那么 dp[i - 1] 里面存的就是第 1 项到第 i - 1 项区间内所有元素的和，那么可得递推公式： dp[i] = dp[i - 1] + arr[i - 1] ；
  - 这里的递推公式有几个需要注意的点：
    1. 为什么加的是 arr[i - 1]？
      - 因为数组下标是从 0 开始的，所以 “第 1 项元素” 在数组中是 arr[0]，第 i 项元素在数组中就是 arr[i - 1]，这也就是为什么递推公式中加的是 arr[i - 1]。
    2. dp[0] 的值需要初始化为 0。
  所以前缀和的计算模板为：
  1
  2
  3
  for (int i = 1; i <= nums.length; i++) {
  dp[i] = dp[i - 1] + nums[i - 1]; // 前缀和
  }
2. 使用前缀和数组，快速求出某⼀个区间内所有元素的和：当询问的区间是第 left 项到第 right 项时：区间内所有元素的和为： dp[right] - dp[left - 1]。
  - 如果我们想知道第 1 项到第 i 项区间内所有元素的和，根据上面的式子，那就是 dp[i] - dp[0]，因为 dp[0] = 0，所以第 1 项到第 i 项区间内所有元素的和就是 dp[i]，和前面的定义相呼应，这也就是为什么 dp[0] 需要初始化为 0。
为了便于理解，以下面的数组为例：
1. 首先在初始化前缀和数组 dp 的时候，根据前面的计算模板，完成前缀和数组的初始化。
2. 然后通过前缀和数组，就能快速地得到某段区间内的所有元素和。例如，如果想知道第 2 项到第 6 项区间内的元素和，那就是 dp[6] - dp[1] = 18 - 2 = 16。
![](../../../../../Running Noob/计算机/Typora笔记/笔记-git仓库/LeetCode-notebook/img/前缀和/前缀和例子.png)
- 一定要注意第 i 项元素在 arr 数组中是 arr[i - 1]，所以如果想求 arr 数组下标为 [i, j] 区间内的元素和，那求的就是第 i+1 项到第 j+1 项区间内的元素和，那就是 dp[j + 1] - dp[i]。
  建议在面对求数组某段区间内的元素和时，先转换为求第 left 项到第 right 项区间内的元素和，再套入公式 dp[right] - dp[left - 1]，就不容易出错了。

1.【模板】前缀和

题目

描述
给定一个长度为 n 的数组 𝑎1,𝑎2,….𝑎𝑛
接下来有 q 次查询, 每次查询有两个参数 l, r.
对于每个询问, 请输出 𝑎𝑙+𝑎(𝑙+1)+….+𝑎𝑟
输入描述：
第一行包含两个整数 n 和 q.
第二行包含 n 个整数, 表示 𝑎1,𝑎2,….𝑎𝑛
接下来 q 行,每行包含两个整数 l 和 r.
1≤𝑛,𝑞≤10^5
−10^9≤𝑎[𝑖]≤10^9
1≤𝑙≤𝑟≤𝑛
输出描述：
输出q行,每行代表一次查询的结果.
示例1
输入：
1
2
3
4
3 2
1 2 4
1 2
2 3
输出：
1
2
3
6

思路

前缀和的模板题，根据前面的理论基础，可以很容易得到下面的代码：

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int q = in.nextInt();
        int[] nums = new int[n];
        long[] dp = new long[n + 1];
        for (int i = 0; i < n; i++) {
            nums[i] = in.nextInt();
            dp[i + 1] = dp[i] + nums[i]; // 前缀和
        }
        for (int i = 0; i < q; i++) {
            int l = in.nextInt();
            int r = in.nextInt();
            System.out.println(dp[r] - dp[l - 1]);
        }
    }
}

注意 −10^9≤𝑎[𝑖]≤10^9，所以 nums 数组用 int 类型是没问题的，但是 dp 数组需要用 long 类型来存储，因为 dp 数组存储的是和，用 int 类型可能会有溢出问题。

这题如果用暴力解法，那每一轮查询都要遍历计算一次，时间复杂度为 O(q * n)，而用前缀和，就将时间复杂度降低到 O(n)。

2.寻找数组的中心下标

题目

给你一个整数数组 nums ，请计算数组的 中心下标 。

数组 中心下标 是数组的一个下标，其左侧所有元素相加的和等于右侧所有元素相加的和。

如果中心下标位于数组最左端，那么左侧数之和视为 0 ，因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。

如果数组有多个中心下标，应该返回 最靠近左边 的那一个。如果数组不存在中心下标，返回 -1 。

示例 1：

输入：nums = [1, 7, 3, 6, 5, 6]
输出：3
解释：
中心下标是 3 。
左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 ，
右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ，二者相等。

示例 2：

输入：nums = [1, 2, 3]
输出：-1
解释：
数组中不存在满足此条件的中心下标。

示例 3：

输入：nums = [2, 1, -1]
输出：0
解释：
中心下标是 0 。
左侧数之和 sum = 0 ，（下标 0 左侧不存在元素），
右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0 。

提示：

1 <= nums.length <= 104
-1000 <= nums[i] <= 1000

思路

class Solution {
    public int pivotIndex(int[] nums) {
        int res = -1;
        int[] dp = new int[nums.length + 1];
        for (int i = 0; i < nums.length; i++) {
            dp[i + 1] = dp[i] + nums[i]; // 前缀和
        }
        for (int i = 0; i < nums.length; i++) {
            // 下标为 i 表示的是第 i+1 项
            // 第 i+1 项左端之和那就是第 1 项到第 i 项, 代入公式为：dp[i] - dp[0]
            // 第 i+1 项右端之和那就是第 i+2 项到第 nums.length 项, 代入公式为：dp[nums.length] - dp[i + 1]
            if (dp[i] - dp[0] == dp[nums.length] - dp[i + 1]) {
                res = i;
                break;
            }
        }
        return res;
    }
}

这题就体现出把数组下标 i 和第 i+1 项对应起来的重要性，否则可能就容易搞乱。

3.除自身以外数组的乘积(前缀积+后缀积)

题目

给你一个整数数组 nums，返回数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。
题目数据保证数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法，且在 O(n) 时间复杂度内完成此题。
示例 1:
1
2
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:
1
2
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
提示：
- 2 <= nums.length <= 105
- -30 <= nums[i] <= 30
- 保证数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内

思路

注意题目的要求，不能使用除法，并且要在 O(N) 的时间复杂度内完成该题。那么我们就不能使用暴力的解法，以及求出整个数组的乘积，然后除以单个元素的方法。继续分析，根据题意，对于每⼀个位置的最终结果 res[i] ，它是由两部分组成的：

nums[0] * nums[1] * nums[2] * … * nums[i - 1]
nums[i + 1] * nums[i + 2] * … * nums[n - 1]

于是，我们可以利用前缀和的思想，使用两个数组 pre 和 post，分别处理出来两个信息：

pre 表示：i 位置之前的所有元素，即 [0, i - 1] 区间内所有元素的前缀乘积
post 表示： i 位置之后的所有元素，即 [i + 1, n - 1] 区间内所有元素的后缀乘积

然后再处理最终结果。

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int[] pre = new int[nums.length + 1];
        int[] post = new int[nums.length + 1];
        int[] answer = new int[nums.length];
        pre[0] = 1;
        for (int i = 1; i <= nums.length; i++) {
            pre[i] = pre[i - 1] * nums[i - 1]; // 前缀积
        }
        post[0] = 1;
        for (int i = 1; i <= nums.length; i++) {
            post[i] = post[i - 1] * nums[nums.length - i]; // 后缀积
        }
        for (int i = 0; i < answer.length; i++) {
            // 求下标为i以外的元素的乘积，就是求第i+1项元素以外的元素乘积
            // 第1项到第i项区间内元素的乘积就是pre[i] / pre[0],因为pre[0]=1,所以就是pre[i]
            // 第i+2项到第n项区间内元素的乘积就是post[nums.length - i - 1] / post[0],因为post[0]=1,所以就是post[nums.length - i - 1]
            answer[i] = pre[i] * post[nums.length - i - 1];
        }
        return answer;
    }
}

前缀积中元素下标 i 和第 i+1 项元素相对应，以及第 left 项到第 right 项的积的计算公式 pre[right] / pre[left - 1] 是已经比较明确清楚的。后缀积的计算公式则需要做一些小小的转换。
在后缀积中，由于是从后向前乘，所以第 left 项到第 right 项的积的计算公式为：post[nums.length - (left - 1)] / post[nums.length - right]
- 由于本题中求的是第 i+2 项到第 n 项区间内元素的乘积，所以就是 post[nums.length - ((i + 2) - 1) / post[nums.length - nums.length] = post[nums.length - i - 1] / post[0]。

**注意：只需要记住前缀积的公式是 dp[right] / dp[left - 1]，那么后缀积的公式就是 dp[nums.length - (left - 1)] / dp[nums.length - right]**，前提是后缀积的数组在初始化时也是从前向后初始化。

4.★和为 k 的子数组

题目

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的子数组的个数 。
子数组是数组中元素的连续非空序列。
示例 1：
1
2
输入：nums = [1,1,1], k = 2
输出：2
示例 2：
1
2
输入：nums = [1,2,3], k = 3
输出：2
提示：
- 1 <= nums.length <= 2 * 10^4
- -1000 <= nums[i] <= 1000
- -10^7 <= k <= 10^7

思路

第一种思路，暴力解法，i 指定区间的起始位置，j 指定区间的终止位置，k 从 i 遍历到 j，计算 [i, j] 区间的元素和，判断是否和 k 相等，时间复杂度为 O(n^3)，肯定是不可取的。

第二种思路，用前缀和降低时间复杂度，相当于把 “k 从 i 遍历到 j” 这一步给去掉了，时间复杂度为 O(n^2)。

class Solution {
    public int subarraySum(int[] nums, int k) {
        int res = 0;
        int[] dp = new int[nums.length + 1];
        for (int i = 1; i <= nums.length; i++) {
            dp[i] = dp[i - 1] + nums[i - 1]; // 前缀和
        }
        for (int i = 0; i < nums.length; i++) {
            for (int j = i; j < nums.length; j++) {
                // 第i+1项到第j+1项元素和
                if (dp[j + 1] - dp[i] == k) {
                    res++;
                }
            }
        }
        return res;
    }
}

提交发现，虽然能通过，但是耗时很长。

第三种思路，在第二种思路的基础上，进一步优化，时间复杂度可以降低到 O(n)。

设 i 为数组中的任意位置，用 dp[i + 1] 表示 [0, i] 区间内所有元素的和。
想知道有多少个「以下标 i 为结尾的和为 k 的子数组」，就要找到有多少个起始位置为 x1, x2, x3… 使得 [x, i] 区间内的所有元素的和为 k 。
那么 [0, x - 1] 区间内的和是不是就是 dp[i + 1] - k 了。于是问题就变成：
- 在 [0, i - 1] 区间内，找到有多少前缀和等于 dp[i + 1] - k 即可。
我们不用真的初始化⼀个前缀和数组，因为我们只关心在 i 位置之前，有多少个前缀和等于 dp[i + 1] - k 。因此，我们仅需用⼀个哈希表，⼀边求当前位置的前缀和，⼀边存下之前每⼀种前缀和出现的次数。

class Solution {
    public int subarraySum(int[] nums, int k) {
        int res = 0;
        int sum = 0;
        // key:前缀和；value:相同的前缀和的个数
        Map<Integer, Integer> preSumFreq = new HashMap<>();
        preSumFreq.put(0, 1);
        for (int i = 0; i < nums.length; i++) {
            sum += nums[i];
            if (preSumFreq.containsKey(sum - k)) { // 如果存在前缀和 = dp[i+1] - k
                res += preSumFreq.get(sum - k);
            }
            preSumFreq.put(sum, preSumFreq.getOrDefault(sum, 0) + 1);
        }
        return res;
    }
}

对于一开始的情况，下标 0 之前没有元素，可以认为前缀和为 0，个数为 1 个，因此 preSumFreq.put(0, 1);，这一点是必要且合理的。
- 具体的例子是：nums = [3,...], k = 3

4.2 和可被 K 整除的子数组

题目

给定一个整数数组 nums 和一个整数 k ，返回其中元素之和可被 k 整除的非空 子数组 的数目。
子数组 是数组中连续的部分。
示例 1：
1
2
3
4
5
输入：nums = [4,5,0,-2,-3,1], k = 5
输出：7
解释：
有 7 个子数组满足其元素之和可被 k = 5 整除：
[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]
示例 2:
1
2
输入: nums = [5], k = 9
输出: 0
提示:
- 1 <= nums.length <= 3 * 10^4
- -10^4 <= nums[i] <= 10^4
- 2 <= k <= 10^4

思路

会发现这题和 4.和为 k 的子数组 很像，其实是同一个套路，但是要稍微变通一下。
同余定理：如果 (a - b) % n == 0 ，那么我们可以得到⼀个结论： a % n == b % n 。用文字叙述就是，如果两个数相减的差能被 n 整除，那么这两个数对 n 取模的结果相同。
- 设 i 为数组中的任意位置，用 dp[i + 1] 表示 [0, i] 区间内所有元素的和。
- 想知道有多少个「以 i 为结尾的可被 k 整除的子数组」，就要找到有多少个起始位置为 x1,x2, x3… 使得 [x, i] 区间内的所有元素的和可被 k 整除。
- 设 [0, x - 1] 区间内所有元素之和等于 a ， [0, i] 区间内所有元素的和等于 b ，可得 (b - a) % k == 0
  - 根据同余定理，上式转变为：b % k == a % k
  于是问题就变成：
  - 找到在 [0, i - 1] 区间内，有多少前缀和的余数等于 dp[i + 1] % k 的即可。
  这样，这个问题就和 4.和为 k 的子数组 几乎一模一样了。

class Solution {
    public int subarraysDivByK(int[] nums, int k) {
        int res = 0;
        int sum = 0;
        // Map<前缀和 % k, 前缀和 % k 的值相同的个数>
        Map<Integer, Integer> preModFreq = new HashMap<>();
        preModFreq.put(0, 1);
        for (int i = 0; i < nums.length; i++) {
            sum += nums[i];
            int mod = (sum % k + k) % k; // 对负值进行修正
            if (preModFreq.containsKey(mod)) {
                res += preModFreq.get(mod);
            }
            preModFreq.put(mod, preModFreq.getOrDefault(mod, 0) + 1);
        }
        return res;
    }
}

有一个需要注意的点是：负数取模的结果需要被修正，例如 - 1 % 2，Java 做取模运算的时候，a % b = a - a / b * b，所以 - 1 % 2 = -1 - (-1 / 2 * 2) = -1，在本题需要将负数修正为正数，所以存入 map 中的 key 不是 sum % k，而是 (sum % k + k) % k。

当 k 的值不大的时候，我们甚至还能进一步对上述的代码进行优化，用数组代替哈希表，能进一步优化执行时间：

class Solution {
    public int subarraysDivByK(int[] nums, int k) {
        int res = 0;
        int sum = 0;
        int[] preModFreq = new int[k];
        preModFreq[0] = 1;
        for (int i = 0; i < nums.length; i++) {
            sum += nums[i];
            int mod = (sum % k + k) % k; // 对负值进行修正
            res += preModFreq[mod];
            preModFreq[mod]++;
        }
        return res;
    }
}

4.3 连续数组

题目

给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组，并返回该子数组的长度。

示例 1:

1
2
3

输入: nums = [0,1]
输出: 2
说明: [0, 1] 是具有相同数量 0 和 1 的最长连续子数组。

示例 2:

1
2
3

输入: nums = [0,1,0]
输出: 2
说明: [0, 1] (或 [1, 0]) 是具有相同数量0和1的最长连续子数组。

提示：

1 <= nums.length <= 10^5
nums[i] 不是 0 就是 1

思路

稍微转化⼀下题目，就会变成我们熟悉的题：
- 由于「0 和 1 的数量相同」等价于「1 的数量减去 0 的数量等于 0」，我们可以将数组中的 0 视作 −1，则原问题转换成「求最长的连续子数组，其元素和为 0」。
- 那这题就和 4.和为 k 的子数组 完全相同了，只不过这题为 “和为 0 的子数组”，而且 4.和为 k 的子数组 求的是和为 k 的子数组的个数，而本题求的是和为 0 的最大连续子数组的长度。
设 i 为数组中的任意位置，用 dp[i + 1] 表示 [0, i] 区间内所有元素的和。
- 想知道最大的「以 i 为结尾的和为 0 的子数组」，就要从左往右找到第⼀个 x1 使得 [x1, i] 区间内的所有元素的和为 0 。那么 [0, x1 - 1] 区间内的和是不是就是 dp[i + 1] 了。于是问题就变成：
  - 找到在 [0, i - 1] 区间内，第⼀次出现 dp[i + 1] 的位置。
我们不用真的初始化⼀个前缀和数组，因为我们只关心在 i 位置之前，第⼀个前缀和等于 dp[i + 1] 的位置。因此，我们仅需用⼀个哈希表，⼀边求当前位置的前缀和，⼀边记录第⼀次出现该前缀和的位置。

class Solution {
    public int findMaxLength(int[] nums) {
        int res = 0;
        int sum = 0;
        // Map<前缀和, 相同的前缀和第一次出现的位置>
        Map<Integer, Integer> preSumMap = new HashMap<>();
        // 针对的是这种例子: [0,1,...], 此时 i = 1, sum = 0, 为了得到长度为 2, 
        // 就需要 i - preSumMap.get(sum) = 1 - preSumMap.get(0) = 2, 则 preSumMap.get(0) = -1
        preSumMap.put(0, -1);
        for (int i = 0; i < nums.length; i++) {
            sum += (nums[i] == 0 ? -1 : 1);
            if (preSumMap.containsKey(sum)) {
                // 如果之前存在前缀和为sum, 说明从那之后的连续子数组的和为0
                res = Math.max(res, i - preSumMap.get(sum));
            } else {
                // 记录该前缀和第一次出现的位置
                preSumMap.put(sum, i);
            }
        }
        return res;
    }
}

注意本题和 4.和为 k 的子数组 的区别：
- 4.和为 k 的子数组 中的 Map 是 Map<前缀和, 相同的前缀和的个数>
- 本题中的 Map 是 Map<前缀和, 相同的前缀和第一次出现的位置>

5.【模板】二维前缀和

题目

描述
给你一个 n 行 m 列的矩阵 A ，下标从 1 开始。
接下来有 q 次查询，每次查询输入 4 个参数 x1 , y1 , x2 , y2
请输出以 (x1, y1) 为左上角 , (x2,y2) 为右下角的子矩阵的和
输入描述：
第一行包含三个整数n,m,q.
接下来n行，每行m个整数，代表矩阵的元素
接下来q行，每行4个整数x1, y1, x2, y2，分别代表这次查询的参数
1≤𝑛,𝑚≤1000
1≤𝑞≤10^5
−10^9≤𝑎[𝑖][𝑗]≤10^9
1≤𝑥1≤𝑥2≤𝑛
1≤𝑦1≤𝑦2≤𝑚
输出描述：
输出q行，每行表示查询结果。
示例1
输入：
1
2
3
4
5
6
7
3 4 3
1 2 3 4
3 2 1 0
1 5 7 8
1 1 2 2
1 1 3 3
1 2 3 4
输出：
1
2
3
8
25
32
备注：读入数据可能很大，请注意读写时间。

思路

和一维前缀和的原理类似，只不过二维前缀和求的是一个矩阵中所有元素的和。
- 例如：对与 x = 4，y = 3 这么一组输入，就是将原矩阵序列中蓝色区域的元素相加，得到的结果便是前缀和矩阵 dp 中 dp[ 4 ][ 3 ] 的值。
例如下图，我们要求蓝色矩阵中所有元素的和。
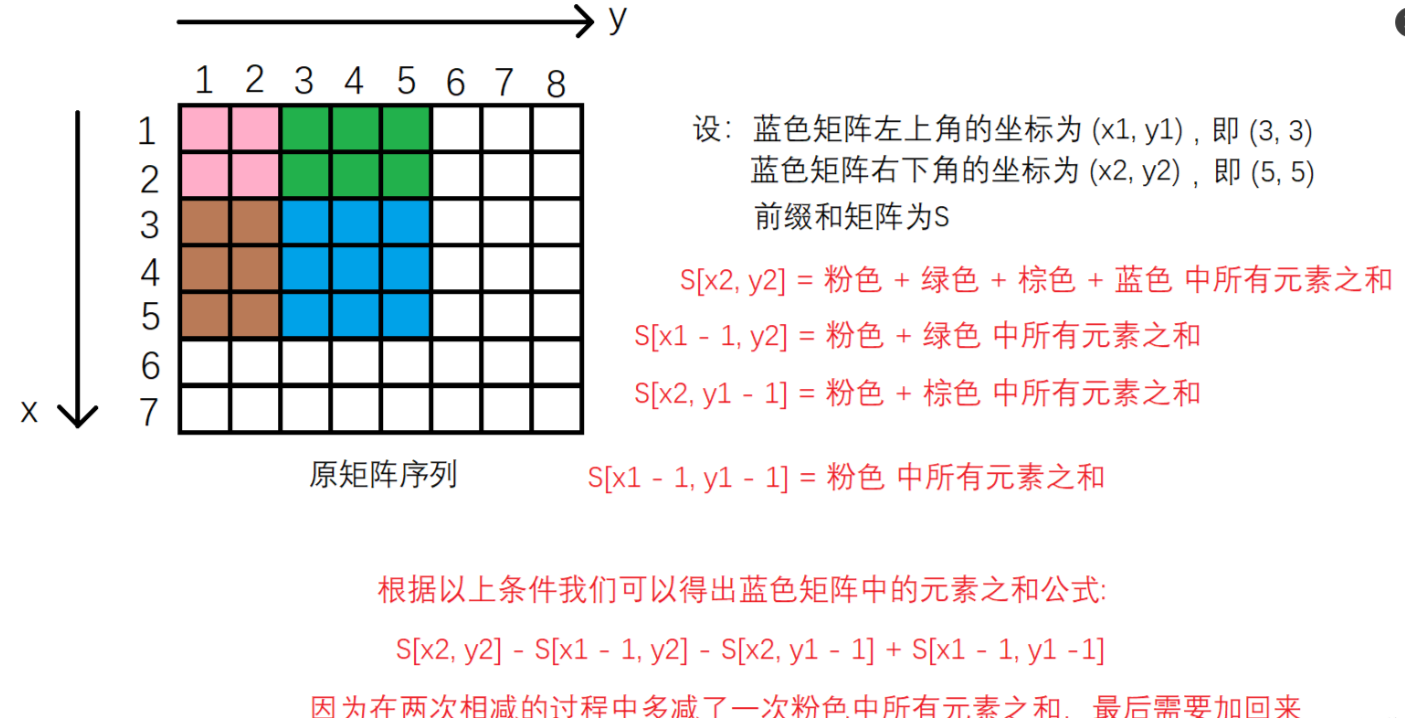
那么我们应该怎么得到这个前缀和矩阵？
- 同理利用递推关系求就可以了：dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + nums[i - 1][j - 1];。

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int m = in.nextInt();
        int q = in.nextInt();
        int[][] nums = new int[n][m]; // 其实完全可以不用定义nums数组，直接在输入的过程中就可以把前缀和矩阵给填充好
        long[][] dp = new long[n + 1][m + 1];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                nums[i][j] = in.nextInt();
            }
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + nums[i - 1][j - 1];
            }
        }
        while (q > 0) {
            int x1 = in.nextInt();
            int y1 = in.nextInt();
            int x2 = in.nextInt();
            int y2 = in.nextInt();
            long result = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1];
            System.out.println(result);
            q--;
        }
    }
}

5.2 矩阵区域和

题目

给你一个 m x n 的矩阵 mat 和一个整数 k ，请你返回一个矩阵 answer ，其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和：
- i - k <= r <= i + k,
- j - k <= c <= j + k 且
- (r, c) 在矩阵内。
示例 1：
1
2
输入：mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出：[[12,21,16],[27,45,33],[24,39,28]]
示例 2：
1
2
输入：mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2
输出：[[45,45,45],[45,45,45],[45,45,45]]
提示：
- m == mat.length
- n == mat[i].length
- 1 <= m, n, k <= 100
- 1 <= mat[i][j] <= 100

思路

⼆维前缀和的简单应用题，关键就是我们在填写结果矩阵的时候，要找到原矩阵对应区域的「左上角」以及「右下角」的坐标。

左上角坐标： x1 = i - k ， y1 = j - k ，但是由于会「超过矩阵」的范围，因此需要进行修正。
右下角坐标： x2 = i + k ， y2 = j + k ，但是由于会「超过矩阵」的范围，因此需要进行修正。

然后将求出来的坐标代⼊到「二维前缀和矩阵」的计算公式上即可。

class Solution {
    public int[][] matrixBlockSum(int[][] mat, int k) {
        int m = mat.length;
        int n = mat[0].length;
        int[][] dp = new int[m + 1][n + 1]; // 二维前缀和矩阵
        int[][] res = new int[m][n];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + mat[i - 1][j - 1];
            }
        }
        for (int i = 1; i <= m; i++) {
            int x1 = i - k < 1 ? 1 : i - k; // 边界判断
            int x2 = i + k > m ? m : i + k; // 边界判断
            for (int j = 1; j <= n; j++) {
                int y1 = j - k < 1 ? 1 : j - k; // 边界判断
                int y2 = j + k > n ? n : j + k; // 边界判断
                res[i - 1][j - 1] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1];
            }
        }
        return res;
    }
}