- 研究场景:针对 DNN(深度神经网络)应用
- 研究目标:降低能耗,满足 deadline 和 budget 约束
- 放置策略:混合的混沌进化算法,将阿基米德最优化算法、模拟退火法、遗传算法混合起来,并选择性地使用 DVFS 技术
Introduction
该论文的 introduction 是按以下的逻辑顺序来进行阐述的:
- 首先介绍该论文的研究场景是针对 DNN 应用,所以简单介绍了 DNN 应用并使用 “层” 来描述 DNN 应用。
- 然后提出 DNN 应用在移动设备端执行和在云端执行的不足之处,以此来引出 MEC(Mobile Edge Computing)。
- 指出在 MEC 环境下,需要考虑诸多性能指标,包括能耗、deadline 和 budget。
- 介绍降低能耗的技术 DVFS,并指出 DVFS 可能的不适用场景,以及使用 DVFS 技术后需要考虑的和其他性能指标的权衡。
- 介绍元启发式算法,包括阿基米德最优化算法 AOA、模拟退火法 SA、遗传算法 GA,介绍它们具体的优势和不足之处。
- 最终介绍该论文所提出的放置策略:混合的混沌进化算法 HCEA,并罗列该论文的 contributions。
可以看到,introduction 的书写就是按照研究场景、研究目标、放置策略这条线来进行简要概述的,可以学习这种写作方式。
System Model and Problem Formulation
- 符号列张符号表
System Architecture
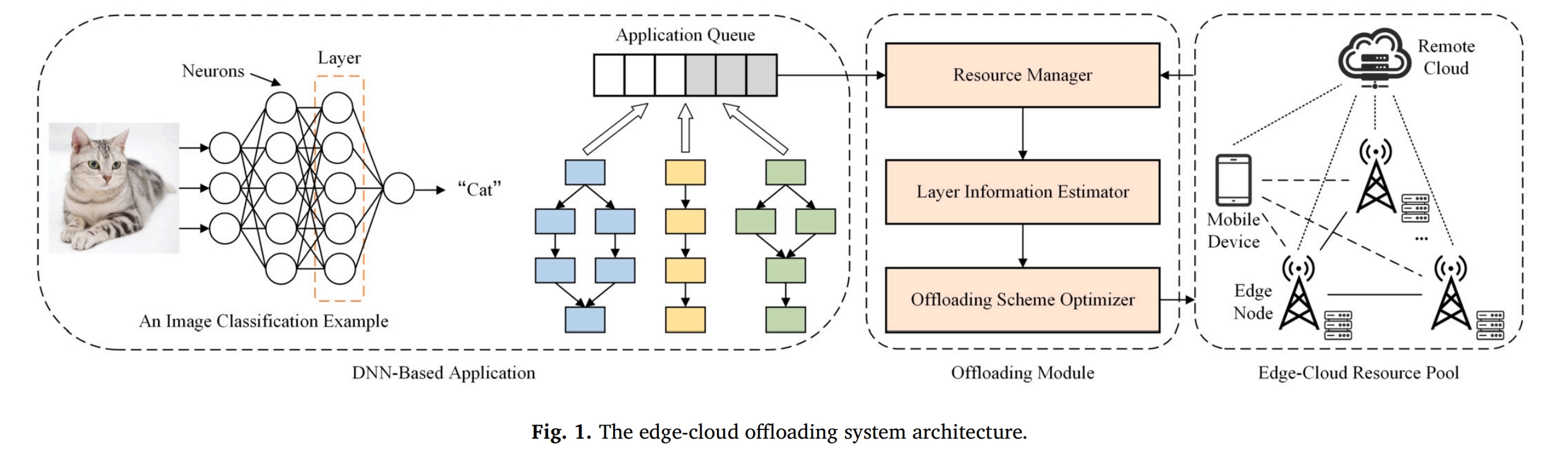
系统结构主要由这几部分组成:
- Application Queue:用于保存提交的 DNN 应用程序
- Resource Manager:资源监控与协调
- Layer Information Estimator:计算 DNN 应用程序层执行的相关参数
- Offloading Scheme Optimizer:产生放置策略
Edge - Cloud 资源池包括:
- 移动设备
- 多个边缘计算节点
- 远端云
资源池中的资源用
描述,对于 - 最大处理能力是
- 单位租赁计费是
- 资源类型是
, ,0 表示移动设备,1 表示边缘计算节点,2 表示云端 和 之间带宽是 - 对于存储,假设可以满足
- 执行频率集合
, , - 当计算资源处于
执行频率时,其处理能力为
- 当计算资源处于
DNN-based Application Model
以层的方式来描述 DNN 应用,每一层都包含一个或多个神经元。
对于 DNN 应用程序集合,
每一个 DNN 应用程序都可以被表示为一个有向无环图,
表示应用程序层的集合 - 第
层的计算负载为
- 第
表示应用程序层之间的数据依赖关系 表示 对应的数据传输量
Problem Formulation
makespan
在 上的执行时间为: , 是 当前的工作频率。 对于
在 上执行, 在 上执行,数据传输时间为:$TT_i^{p,j} = \left{ \right.$ 在 上的开始时间和结束时间: , 是 的可获得时间
对于第 i 个 DNN 应用,其完成时间为:
rental cost
指的是被放置到 上进行服务执行的 DNN 应用程序 “层” 所以对于
,其租赁计费即为其开始启动的时间 到 其结束执行关机的时间
energy consumption
- 能耗暂时不是我们考虑的放置目标
offloading problem
- 对于将 DNN 应用程序卸载到计算资源节点上的问题,目标在于确定 DNN 的 “层” 和计算资源节点的对应关系,同时确定 “层” 的执行顺序和计算资源节点的执行频率。
Proposed Algorithm
该论文提出的算法是混合的混沌进化算法 HCEA(a Hybrid Chaotic Evolutionary Algorithm) 及其 DVFS 版本 HCEA-DVFS,下面是 HCEA 的图示:
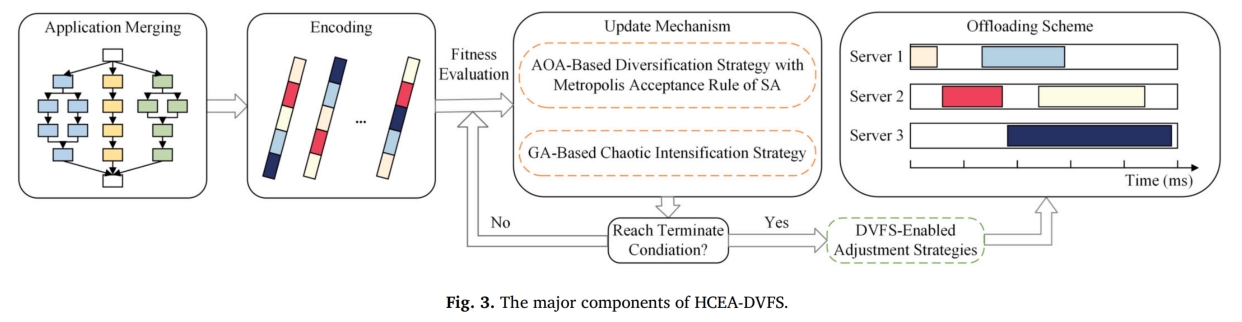
- 算法在种群初始化时使用了混沌序列来提高初始种群的质量,并在种群更新过程中引入随机性。
- 在种群进化过程中,使用 AOA-based 多样化策略来探索解空间,而且在原来的 AOA 算法的基础之上,同时引入全局(对整个种群)和局部(对物体自身历史)最优解来加速搜索更优解。
- 使用 SA 的 Metropolis acceptance rule 来避免算法陷入局部最优。
- 使用 GA 的混沌增强策略来增强对解周围局部空间的搜索。
- 基于用户给出的约束,使用一个更宽松的约束,来期望找到潜在的更优解。
- 使用 DVFS 来降低能耗。
encoding and initialization
对于种群中的每个物体
,其都代表一个解,其位置向量 代表了 DNN 应用 “层” 和计算资源节点之间的映射关系。 表示第 i 个 DNN 应用的第 2 “层” 被放置在第 3 个计算资源节点 上。
除了位置向量,每个物体还有体积、密度和加速度向量:
- 体积:
- 密度:
- 加速度:
在种群初始化时,每个物体的位置、体积、密度、加速度都会被初始化,而且会使用
tent map(帐篷映射,混沌映射的一种)进行初始化,使得种群具有良好的分布性和随机性。- 因为有四个向量,所以对应有四个混沌序列,它们都是用
tent map来生成的:$\delta_{j+1}^k = \left{\right.,\forall k \in {1,2,3,4}$
- 因为有四个向量,所以对应有四个混沌序列,它们都是用
decoding
- 论文中的 decoding 就是说,在得到了放置解之后,执行时间,租赁开销和能耗就可以评估了。
fitness evaluation
- 适应值的计算是要根据你的研究目标来确定的,该论文的研究目标是能耗、deadline 和 budget 约束,所以应该从这几个角度来考虑。
- 这篇论文并没有用经典的对几个研究目标进行加权,而是设计了新的适应值评估方法,这应该也是该论文的创新点之一。
- 新的适应值评估方法是基于
约束方法,在 exploration 阶段,采用的是宽松的约束,在 exploitation 阶段,采用的是原来的约束。同时,考虑到能耗的研究目标,在比较两个物体的适应值,判断谁更优时,该论文设计了自己的比较方法,详细见论文式(18)。
- 新的适应值评估方法是基于
update mechanism
这篇论文的
diversification strategy基于 AOA,相比于原来的 AOA 只使用了当前种群中的最优解(全局)来引导种群进化的方向,该论文又引入“局部” 最优解来辅助引导种群的进化方向,这个 “局部” 最优解实际上是每个物体在进化过程中,历史上的最优解。- $r_j^t = \left{
\right.$
- $r_j^t = \left{
- $A_i^{t+1} = \left{
\right.$ 分别是种群中随机挑选的个体的密度、体积和加速度。
- 归一化后的加速度:
- $X_i^{t+1} = \left{
\right.$ - $dir = \left{
\right.$
- $dir = \left{
为了避免陷入局部最优,这篇论文还使用了模拟退火法的 Metropolis acceptance rule 来判断是否要更新当前物体的位置:
- $X_i^{t+1} = \left{
\right.$
- $X_i^{t+1} = \left{
这篇论文的
intensification strategy基于 GA,使用交叉和变异算子来在局部空间内进一步 exploitation,同时其中还掺加了 logistic 映射(用 logistic 映射生成的随机数掺杂到交叉概率和变异的变化数中)。- 而且仅仅是对
进行增强操作。
- 而且仅仅是对
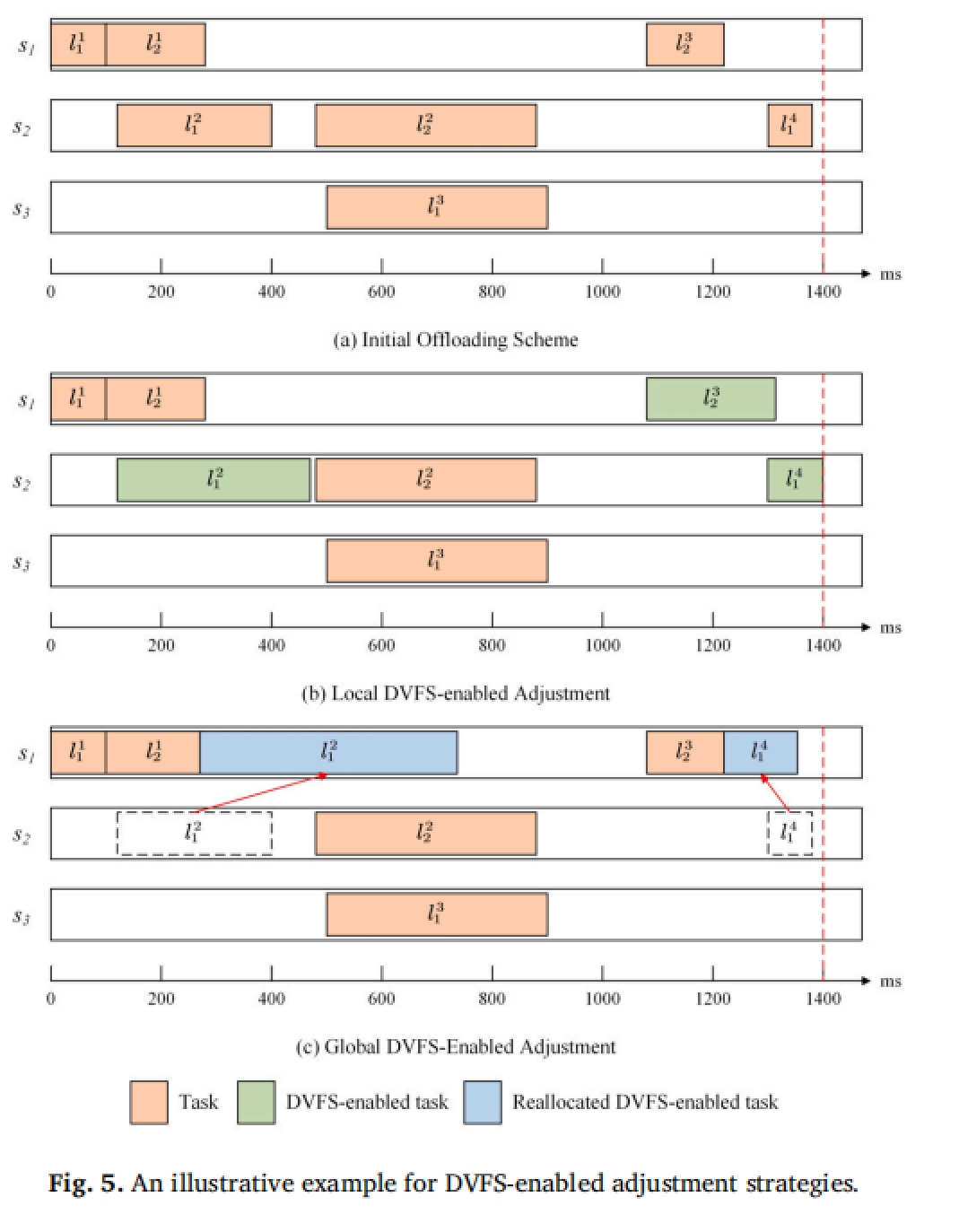
在多样化策略和增强策略之后,就是使用 DVFS 技术进行进一步的降低能耗。该论文的 DVFS 又分为局部 DVFS 和全局 DVFS。
- 局部 DVFS 仅在具体的计算资源节点上调整执行频率,以充分使用计算资源节点的空闲时间,这样能耗可以降低,但是资源的使用时间不变,所以开销也不变。
- 全局 DVFS 则会对 DNN 应用 “层” 进行重新放置,以达到真正的降低能耗和开销。
flowchart
最后看看 HCEA-DVFS 的流程图:
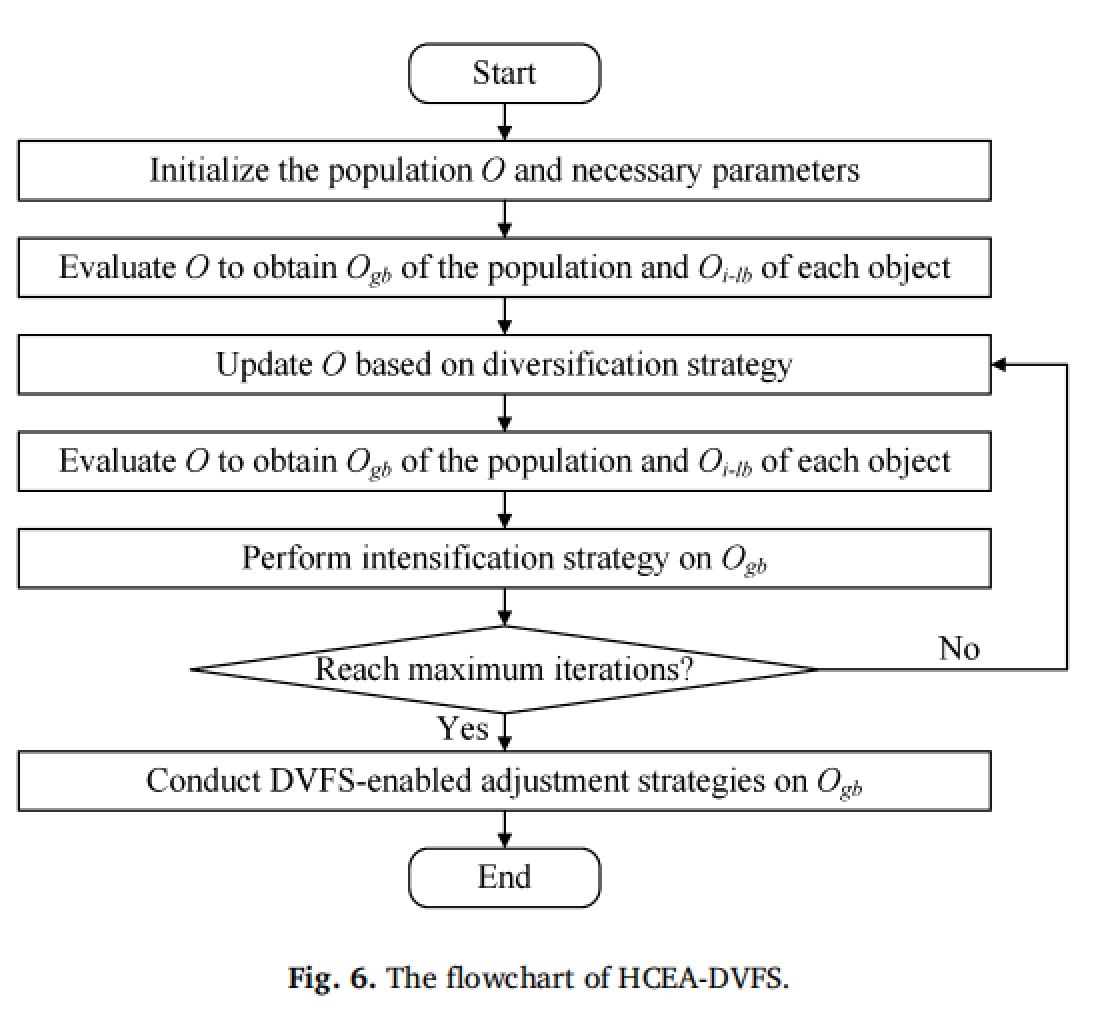
Experimental Results and Analysis
setup
- 参数的选定使用的是田口方法来确定的。
baseline
baseline 总共有 4 个:
- Greedy 贪心算法
- AOA 阿基米德最优化算法
- MCEA(Multi-objective Clustering Evolutionary Algorithm)
- PSO-GA
以 deadline 约束、budget 约束和 DNN 应用的数量作为变量,即二维图的横坐标。
以能耗作为该论文算法和 baseline 之间比较的依据,在满足 deadline 和 budget 约束的前提下,即能耗是二维图的纵坐标。
- 这里就有三组实验了
然后比较算法之间的运行时间,就是第四组实验